
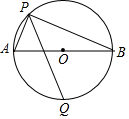
 如图,AB为?O的直径,点P在?O上,AP=6,AB=10,PQ平分∠APB,则PQ=$\frac{97\sqrt{2}}{15}$.
如图,AB为?O的直径,点P在?O上,AP=6,AB=10,PQ平分∠APB,则PQ=$\frac{97\sqrt{2}}{15}$. 分析 直接利用勾股定理得出PB的长进而得出AQ,BQ的长,再利用相似三角形的判定与性质得出PE,EQ的长,进而得出答案.
解答 解:连接AQ,BQ,
∵AP=6,AB=10,
∴PB=8,
∵PQ平分∠APB,
∴∠APQ=∠BPQ,
∴AQ=BQ,
∵AB为?O的直径,
∴△AQB是等腰直角三角形,
∵AB=10,
∴AQ=BQ=$\frac{\sqrt{2}}{2}$×10=5$\sqrt{2}$,
∵∠PAB=∠PQB,∠APE=∠BPQ,
∴△APE∽△QPB,
∴$\frac{AP}{BQ}$=$\frac{PE}{PB}$,
∴$\frac{6}{5\sqrt{2}}$=$\frac{PE}{8}$,
解得:PE=$\frac{24\sqrt{2}}{5}$,
∵∠PAB=∠PQB,∠PEA=∠BEQ,
∴△PAE∽△BQE,
∴$\frac{PA}{BQ}$=$\frac{PE}{BE}$=$\frac{AE}{EQ}$,
∴$\frac{6}{5\sqrt{2}}$=$\frac{\frac{24\sqrt{2}}{5}}{BE}$,
解得:BE=8,
则AE=2,
∴$\frac{6}{5\sqrt{2}}$=$\frac{2}{EQ}$,
解得:EQ=$\frac{5\sqrt{2}}{3}$,
故PQ=PE+EQ=$\frac{24\sqrt{2}}{5}$+$\frac{5\sqrt{2}}{3}$=$\frac{97\sqrt{2}}{15}$.
故答案为:$\frac{97\sqrt{2}}{15}$.
点评 此题主要考查了相似三角形的判定与性质以及圆周角定理,正确应用相似三角形的性质是解题关键.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
 小刚手里有一根长为80cm的木棒,他把木棒垂直放置在地面上(如图所示),此时测出该木棒在太阳光下的影子的长度为60cm,小刚绕木棒与地面的接触点转动该木棒,想尽办法使木棒的影子最长;问:该木棒转到什么位置时影子最长?并求出此时影子的长度.
小刚手里有一根长为80cm的木棒,他把木棒垂直放置在地面上(如图所示),此时测出该木棒在太阳光下的影子的长度为60cm,小刚绕木棒与地面的接触点转动该木棒,想尽办法使木棒的影子最长;问:该木棒转到什么位置时影子最长?并求出此时影子的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
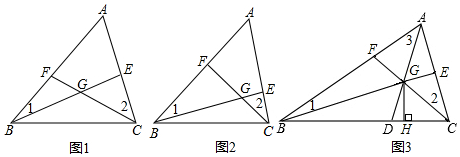
 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,∠ABD与∠C互补.
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,∠ABD与∠C互补.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 400d cm | B. | 300d cm | C. | 304d cm | D. | 301d cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
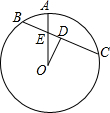 如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.
如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 文具店 | B. | 玩具店 | C. | 文具店西40米处 | D. | 玩具店西60米处 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3)2=3 | B. | (x+3)2=3 | C. | (x-6)2=30 | D. | (x+6)2=30 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点之间线段最短 | B. | 两点确定一条直线 | ||
| C. | 垂线段最短 | D. | 两点之间直线最短 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com