
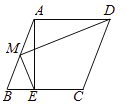
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() 是锐角,
是锐角,![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .若
.若![]() ,则
,则![]() 的值为___________.
的值为___________.
【答案】![]()
【解析】
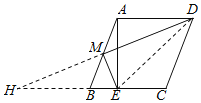
延长DM交CB的延长线于点H.首先证明△ADM≌△BHM,得出AD=HB=4,MD=MH,由线段垂直平分线的性质得出EH=ED,设BE=x,利用勾股定理构建方程求出x,即BE,结合AB得出cosB的值.
解:延长DM交CB的延长线于点H.如图所示:
∵四边形ABCD是菱形,
∴AB=BC=AD=4,AD∥CH,
∴∠ADM=∠H,
∵M是AB的中点,
∴AM=BM,
在△ADM和△BHM中,
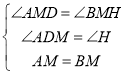 ,
,
∴△ADM≌△BHM(AAS),
∴AD=HB=4,MD=MH,
∵∠EMD=90°,
∴EM⊥DH,
∴EH=ED,
设BE=x,
∵AE⊥BC,
∴AE⊥AD,
∴∠AEB=∠EAD=90°,
∵AE2=AB2-BE2=DE2-AD2,
∴42-x2=(4+x)2-42,
解得:x=![]() ,或x=
,或x=![]() (舍),
(舍),
∴BE=![]() ,
,
∴cosB=![]() .
.
故答案为:![]() .
.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
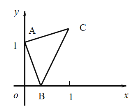
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
A.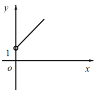 B.
B.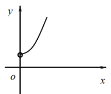
C.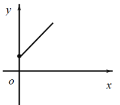 D.
D.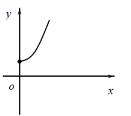
查看答案和解析>>
科目:初中数学 来源: 题型:
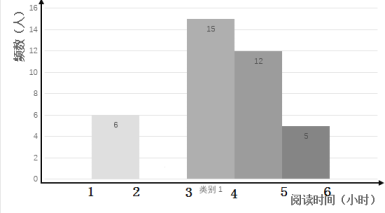
【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
| 6 | 0.12 |
|
| 0.24 |
| 15 | 0.3 |
| 12 |
|
| 5 | 0.1 |
合计 |
| 1 |
(1)求![]() __________,
__________,![]() _________;
_________;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)在![]() 范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第36届全国信息学冬令营在广州落下帷幕,长郡师生闪耀各大赛场,金牌数、奖牌数均稳居湖南省第一.学校拟预算7700元全部用于购买甲、乙、丙三种图书共20套奖励获奖师生,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元,设购买甲种图书x套,乙种图书y套,请解答下列问题:
(1)请求出y与x的函数关系式(不需要写出自变量的取值范围);
(2)若学校购买的甲、乙两种图书共14套,求甲、乙图书各多少套?
(3)若学校购买的甲、乙两种图书均不少于1套,则有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
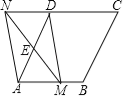
(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 为线段
为线段![]() 上两动点,且
上两动点,且![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() 、
、![]() 的垂线相交于点
的垂线相交于点![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.
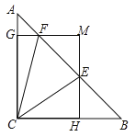
(1)求证:![]() ;
;
(2)试探究![]() 、
、![]() 、
、![]() 之间有何数量关系?说明理由.
之间有何数量关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
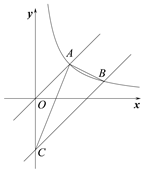
【题目】如图,直线OA与反比例函数![]() (
(![]() )的图像交于点A(3,3),将直线OA沿y轴向下平移,与反比例函数
)的图像交于点A(3,3),将直线OA沿y轴向下平移,与反比例函数![]() (
(![]() )的图像交于点B(6,m),与y轴交于点C.
)的图像交于点B(6,m),与y轴交于点C.
(1)求直线BC的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把八个完全相同的小球平分为两组,每组中每个分别写上1,2,3,4四个数字,然后分别装入不透明的口袋内搅匀,从第一个口袋内取出一个数记下数字后作为点P的横坐标x,然后再从第二个口袋中取出一个球记下数字后作为点P的纵坐标,则点P(x,y)落在直线y=﹣x+5上的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com