
【题目】课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.
我们有多少种剪法,图1是其中的一种方法:

定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
【答案】(1)作图见解析;(2)20或40.
【解析】试题分析:(1)45°自然想到等腰直角三角形,过底角一顶点作对边的高,发现形成一个等腰直角三角形和直角三角形.直角三角形斜边的中线可形成两个等腰三角形,则易得一种情况.第二种情形可以考虑题例中给出的方法,试着同样以一底角作为新等腰三角形的底角,则另一底角被分为45°和22.5°,再以22.5°分别作为等腰三角形的底角或顶角,易得其中作为底角时所得的三个三角形恰都为等腰三角形.即又一三分线作法.
(2)用量角器,直尺标准作30°角,而后确定一边为BA,一边为BC,根据题意可以先固定BA的长,而后可确定D点,再标准作图实验--分别考虑AD为等腰三角形的腰或者底边,兼顾A、E、C在同一直线上,易得2种三角形ABC.根据图形易得x的值.
解:(1)如图所示,

(2)如图3 ①、②作△ABC.


①当AD=AE时,∵2x+x=30+30,∴x=20.
②当AD=DE时,∵30+30+2x+x=180,∴x=40.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】从四边形的一个顶点出发,可得一条对角线;从五边形的一个顶点出发可得二条对角线;从六边形的一个顶点出发可得三条对角线;…按此规律,从n(n≥4,且n是整数)边形的一个顶点出发可得对角线条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=________cm.
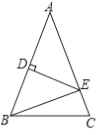
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
(a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
(1)求这条抛物线的表达式;
(2)联结AB、BC、CD、DA,求四边形ABCD的面积;
(3)如果点E在y轴的正半轴上,且∠BEO=∠ABC,求点E的坐标.
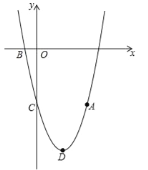
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自来水公司按如下标准收取水费:若每户每月用水不超过10 m3,则每立方米收费1.5元;若每户每月用水超过10 m3,则超过部分每立方米收费2元.小亮家某月的水费不少于25元,那么他家这个月的用水量x(m3)至少是多少?请列出关于x的不等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】((2016北京市)在平面直角坐标系xOy中,点P的坐标为(![]() ,
,![]() ),点Q的坐标为(
),点Q的坐标为(![]() ,
,![]() ),且
),且![]() ,
,![]() ,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
(1)已知点A的坐标为(1,0).
①若点B的坐标为(3,1)求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)⊙O的半径为![]() ,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
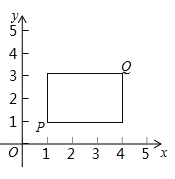
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com