
分析 (1)利用待定系数法,求出k、n的值,利用图象法即可解决问题;
(2)①由题意可知k+2=-2时,两个交点是同一个点;
②分两种情形,利用图象法即可解决问题;
解答 解:(1)∵x=-4,y=-2,
∴-2=-4+k,
∴k=2,
∴当y=4时,x=$\frac{8}{4}$=2,
∴两函数图象分别交于点(-4,-2)和(2,4),
观察图象可知,x<-4或0<x<4时,y1<y2,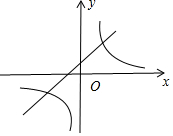
(2)①由题意k+2=-2,
∴k=-4,
②当-4<k<-2时,图象如图所示,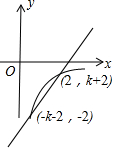
观察图象可知,x>2时,y1>y2,
∴m的最小值为2.
当k>-2时,图象如图所示,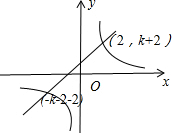
观察图象可知,x>2时,y1>y2,
∴m的最小值为2.
综上所述,m的最小值为2.
点评 本题考查反比例函数与一次函数的交点问题、待定系数法等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题.


科目:初中数学 来源: 题型:选择题
| A. | m≤$\frac{1}{2}$且m≠0 | B. | m<$\frac{1}{2}$且m≠0 | C. | m<$\frac{1}{2}$ | D. | m≤$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
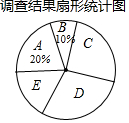 2017年全国两会民生话题成为社会焦点.徐州市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了徐州市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.
2017年全国两会民生话题成为社会焦点.徐州市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了徐州市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.| 组别 | 焦点话题 | 频数(人数) |
| A | 食品安全 | 80 |
| B | 教育医疗 | m |
| C | 就业养老 | n |
| D | 生态环保 | 120 |
| E | 其他 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.
如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com