已知一次函数y=kx+b的图象如图所示.则不等式kx+b＞-1的解集是( )A．x＞-2B．x＜-2C．x＞0D．x＜0 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

18．

已知一次函数y=kx+b的图象如图所示，则不等式kx+b＞-1的解集是（　　）

A．

x＞-2

B．

x＜-2

C．

x＞0

D．

x＜0

分析一次函数的y=kx+b图象经过点（0，-1），由函数表达式可得，kx+b＞-1其实就是一次函数的函数值y＞-1，结合图象可以看出答案．

解答解：由图可知：当x＜0时，y＞-1，即kx+b＞-1；
因此kx+b＞-1的解集为：x＜0．
故选D

点评本题考查了数形结合的数学思想，即学生利用图象解决问题的方法，这也是一元一次不等式与一次函数知识的具体应用．易错易混点：学生往往由于不理解不等式与一次函数的关系或者不会应用数形结合，盲目答题，造成错误．

练习册系列答案

天利38套高中名校期中期末联考测试卷系列答案

口算题应用题天天练神机妙算系列答案

应用题点拨系列答案

培优新方法系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

8．武汉某道路改造工程，若由甲、乙两工程队合作20天可完成；若甲工程队先单独施工40天，再由乙工程队单独施工10天也可完成．
（1）求甲、乙两工程队单独完成此项工程各需要多少天？
（2）如果甲工程队施工每天需付施工费1万元，乙工程队施工每天需付施工费2.5万元，并且要求整个工期不能超过30天，问如何安排甲、乙工程队做这项工程使得花费最少？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．

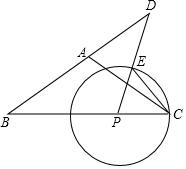如图，在△ABC中，AB=AC=5，cosB=$\frac{4}{5}$，点P为边BC上一动点，过点P作射线PE交射线BA于点D，∠BPD=∠BAC，以点P为圆心，PC长为半径作⊙P交射线PD于点E，联结CE，设BD=x，CE=y．
（1）当⊙P与AB相切时，求⊙P的半径；
（2）当点D在BA的延长线上时，求y关于x的函数解析式，并写出它的定义域；
（3）如果⊙O与⊙P相交于点C、E，且⊙O经过点B，当OP=$\frac{5}{4}$时，求AD的长．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．

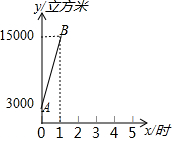为节约能源，某市众多车主响应号召，将燃油汽车改装为天然气汽车．某日上午7：00-8：00，燃气公司给该市城西加气站的储气罐加气，8：00 加气站开始为前来的车辆加气．储气罐内的天然气总量y（立方米）随加气时间x（时）的变化而变化．

时刻	8：00	9：00	10：00	11：00	12：00
y（立方米）	15000	7500	5000	3750	3000

（1）在7：00-8：00 范围内，y随x的变化情况如图所示，求y关于x的函数解析式；
（2）在8：00-12：00 范围内，y的变化情况如下表所示，请写出一个符合表格中数据的y关于x的函数解析式，依此函数解析式，判断上午9：05到9：20能否完成加气950立方米的任务，并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

13．已知点P和点Q在数轴上的位置如图，设点P，Q，N对应的实数分别为p，q，n，且pq=n，则点N作数轴上的位置可能是（　　）

	A．			B．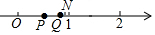
	C．			D．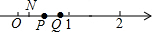

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．

如图，某学校为了加固一篮球架，在下面焊接了一根钢筋撑杆AC，它与水平的钢板箱体成60°的夹角，且AB=0.5m．原有的上撑杆DE=1.6m，且∠BDE=135°．
（1）求撑杆AC的长；
（2）若篮板是边长为1m的正方形，上撑杆端点E在其中心位置，球篮连接篮板处为F，且EF=$\frac{1}{4}$m，下面的钢板箱体厚度为0.3m，CD=1.8m，则点F距地面的高度约为多少米？（结果精确到0.1m，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

10．

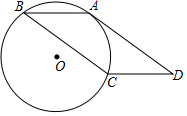如图，?ABCD的边AD与经过A，B，C三点的⊙O相切，sin∠D=$\frac{5}{13}$，AD=24，则⊙O的半径为$\frac{169}{10}$．