
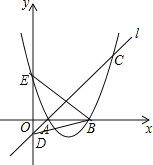
【题目】如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).

(1)求抛物线的解析式;
(2)设直线l与y轴交于点D,抛物线交y轴于点E,则△DBE的面积是多少?
【答案】(1)y=x2﹣4x+3;
(2)△DBE的面积=6.
【解析】
试题分析:(1)把A点和C点坐标代入y=ax2+bx+3可得到关于a、b的方程组,然后解方程求出a、b即可得到抛物线解析式;
(2)先利用待定系数法求出直线l的解析式,再利用坐标轴上点的坐标特征求出D、E、A、B的坐标,然后根据三角形面积公式求解.
解:(1)∵抛物线y=ax2+bx+3经过点A(1,0),点C(4,3),
∴![]() ,解得
,解得![]()
所以抛物线的解析式为y=x2﹣4x+3;
(2)设直线l的解析式为y=kx+m(k≠0),
把A(1,0),点C(4,3)代入得![]() ,解得
,解得![]() ,
,
∴直线l的解析式为y=x﹣1,
当x=0时,y=x﹣1=﹣1,则D(0﹣1),
当x=0时,y=x2﹣4x+3=3,则E(0,3),当y=0时,x2﹣4x+3=3,解得x1=1,x2=3,则B(3,0),
∴△DBE的面积=![]() ×(3+1)×3=6.
×(3+1)×3=6.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】用四舍五入法按要求对0.05019分别取近似值,其中错误的是( )
A. 0.1(精确到0.1) B. 0.05(精确到千分位)
C. 0.05(精确到百分位) D. 0.0502(精确到0.0001)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展课外体育活动,决定开设A:篮球、B:乒乓球、C:踢毽子、D:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.

(1)样本中最喜欢A项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com