
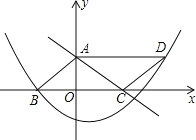
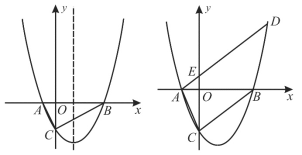
°æƒø°ø»ÁÕº£¨µ„A°¢C∑÷± «“ª¥Œ∫Ø ˝y£Ω©Å![]() x+3µƒÕºœÛ”Îy÷·°¢x÷·µƒΩªµ„£¨µ„B”ε„Cπÿ”⁄‘≠µ„∂‘≥∆£¨∂˛¥Œ∫Ø ˝y£Ω
x+3µƒÕºœÛ”Îy÷·°¢x÷·µƒΩªµ„£¨µ„B”ε„Cπÿ”⁄‘≠µ„∂‘≥∆£¨∂˛¥Œ∫Ø ˝y£Ω![]() x2+bx+cµƒÕºœÛæ≠π˝µ„B£¨«“∏√∂˛¥Œ∫Ø ˝ÕºœÛ…œ¥Ê‘⁄“ªµ„D£¨ πÀƒ±þ–ŒABCDƒÐππ≥…∆Ω––Àƒ±þ–Œ£Æ
x2+bx+cµƒÕºœÛæ≠π˝µ„B£¨«“∏√∂˛¥Œ∫Ø ˝ÕºœÛ…œ¥Ê‘⁄“ªµ„D£¨ πÀƒ±þ–ŒABCDƒÐππ≥…∆Ω––Àƒ±þ–Œ£Æ
£®1£©«Û∂˛¥Œ∫Ø ˝µƒ±Ì¥Ô Ω£ª
£®2£©∂ص„P¥”µ„AµΩµ„D£¨Õ¨ ±∂ص„Q¥”µ„CµΩµ„A∂º“‘√ø√Î1∏ˆµ•ŒªµƒÀŸ∂»‘À∂Ø£¨…Ë‘À∂Ø ±º‰Œ™t√ΣÆ
¢Ÿµ±tŒ™∫Œ÷µ ±£¨”–PQÅAAC£ø
¢⁄µ±tŒ™∫Œ÷µ ±£¨Àƒ±þ–ŒPDCQµƒ√ʪ˝◊Ó–°£ø¥À ±Àƒ±þ–ŒPDCQµƒ√ʪ˝ «∂ý…Ÿ£ø
°æ¥∞∏°ø£®1£©y£Ω![]() x2©Å
x2©Å![]() x©Å3£ª£®2£©¢Ÿµ±t£Ω
x©Å3£ª£®2£©¢Ÿµ±t£Ω![]() √Î ±£¨PQ°ÕAC£¨¢⁄µ±t£Ω
√Î ±£¨PQ°ÕAC£¨¢⁄µ±t£Ω![]() ±£¨Àƒ±þ–ŒPDCQµƒ√ʪ˝◊Ó–°£¨◊Ó–°√ʪ˝Œ™
±£¨Àƒ±þ–ŒPDCQµƒ√ʪ˝◊Ó–°£¨◊Ó–°√ʪ˝Œ™![]()
°æΩ‚Œˆ°ø
£®1£©œ»¿˚”√“ª¥Œ∫Ø ˝µƒΩ‚Œˆ Ω»∑∂®Aµ„∫ÕCµ„◊¯±Í£¨‘Ÿ¿˚”√µ„B”ε„Cπÿ”⁄‘≠µ„∂‘≥∆µ√µΩµ„Bµ„◊¯±Í∫ÕBCµƒ≥§£¨Ω”◊≈¿˚”√∆Ω––Àƒ±þ–Œµƒ–‘÷ «Û≥ˆDµ„◊¯±Í£¨»ª∫Û∞—µ„B∫Õµ„Dµƒ◊¯±Í¥˙»Î∂˛¥Œ∫Ø ˝y£Ω![]() x2+bx+cµ√πÿ”⁄b°¢cµƒ∑Ω≥Ã◊È£¨‘ŸΩ‚∑Ω≥Ã◊È«Û≥ˆb°¢cº¥ø…µ√µΩ∂˛¥Œ∫Ø ˝±Ì¥Ô Ω£ª
x2+bx+cµ√πÿ”⁄b°¢cµƒ∑Ω≥Ã◊È£¨‘ŸΩ‚∑Ω≥Ã◊È«Û≥ˆb°¢cº¥ø…µ√µΩ∂˛¥Œ∫Ø ˝±Ì¥Ô Ω£ª
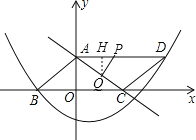
£®2£©¢Ÿœ»¿˚”√π¥π…∂®¿Ìº∆À„≥ˆAC£Ω5£¨‘Ÿ¿˚”√t±Ì æ≥ˆAP£Ωt£¨CQ£Ωt£¨AQ£Ω5©Åt£¨µ±PQ°ÕAC ±ø…÷§√˜°˜APQ°◊°˜CAO£¨‘Ú¿˚”√œýÀ∆±»µ√µΩ![]() £¨Ω‚µ√t£Ω
£¨Ω‚µ√t£Ω![]() £¨»ª∫ÛΩ‚∑Ω≥ëÛ≥ˆtº¥ø…£ª
£¨»ª∫ÛΩ‚∑Ω≥ëÛ≥ˆtº¥ø…£ª
¢⁄◊˜QH°ÕAD”⁄H£¨»ÁÕº£¨œ»÷§√˜°˜AQH°◊°˜CAO£¨¿˚”√œýÀ∆±»ø…±Ì æ≥ˆQH£Ω![]() £®5©Åt£©£¨‘Ÿ∏˘æð»˝Ω«–Œ√ʪ˝π´ Ω£¨¿˚”√SÀƒ±þ–ŒPDCQ£ΩS°˜ACD©ÅS°˜AQPµ√µΩÀƒ±þ–ŒPDCQµƒ√ʪ˝£Ω
£®5©Åt£©£¨‘Ÿ∏˘æð»˝Ω«–Œ√ʪ˝π´ Ω£¨¿˚”√SÀƒ±þ–ŒPDCQ£ΩS°˜ACD©ÅS°˜AQPµ√µΩÀƒ±þ–ŒPDCQµƒ√ʪ˝£Ω![]() t2©Å
t2©Å![]() t+12£¨»ª∫Û∏˘æð∂˛¥Œ∫Ø ˝µƒ–‘÷ «ÛΩ‚£Æ
t+12£¨»ª∫Û∏˘æð∂˛¥Œ∫Ø ˝µƒ–‘÷ «ÛΩ‚£Æ
Ω‚£∫£®1£©µ±x£Ω0£¨y£Ω©Å![]() x+3£Ω3£¨‘Úµ„A£®0£¨3£©£¨
x+3£Ω3£¨‘Úµ„A£®0£¨3£©£¨
µ±y£Ω0£¨©Å![]() x+3£Ω0£¨Ω‚µ√x£Ω4£¨‘Úµ„C£®4£¨0£©£¨
x+3£Ω0£¨Ω‚µ√x£Ω4£¨‘Úµ„C£®4£¨0£©£¨
°þµ„B”ε„Cπÿ”⁄‘≠µ„∂‘≥∆£¨
°ýµ„B£®©Å4£¨0£©£¨BC£Ω8£¨
°þÀƒ±þ–ŒABCD «∆Ω––Àƒ±þ–Œ£¨
°ýAD°Œx÷·£¨AD£ΩBC£Ω8£¨
°ýD£®8£¨3£©£¨
Ω´µ„B£®©Å4£¨0£©£¨µ„D£®8£¨3£©¥˙»Î∂˛¥Œ∫Ø ˝y£Ω![]() x2+bx+cµ√
x2+bx+cµ√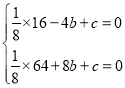 £¨Ω‚µ√
£¨Ω‚µ√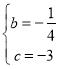 £¨
£¨
°ý∂˛¥Œ∫Ø ˝±Ì¥Ô Ωy£Ω![]() x2©Å
x2©Å![]() x©Å3£ª
x©Å3£ª
£®2£©¢Ÿ°þA£®0£¨3£©£¨C£®4£¨0£©£¨
°ýAC£Ω![]() £Ω5£¨
£Ω5£¨
£¨µ±µ„P‘À∂Ø¡Àt√Î ±£¨‘ÚAP£Ωt£¨CQ
¢⁄◊˜QH°ÕAD”⁄H£¨»ÁÕº£¨
°þ°œHAQ£Ω°œOCA£¨
°ý°˜AQH°◊°˜CAO£¨
°ý![]() £¨º¥
£¨º¥![]() £¨Ω‚µ√QH£Ω
£¨Ω‚µ√QH£Ω![]() £®5©Åt£©£¨
£®5©Åt£©£¨
°ýSÀƒ±þ–ŒPDCQ£ΩS°˜ACD©ÅS°˜AQP
£Ω![]() 38©Å
38©Å![]() t
t![]() £®5©Åt£©
£®5©Åt£©
£Ω![]() t2©Å
t2©Å![]() t+12
t+12
£Ω![]() £®t©Å
£®t©Å![]() £©2+
£©2+![]() £¨
£¨
°ýµ±t£Ω![]() ±£¨Àƒ±þ–ŒPDCQµƒ√ʪ˝◊Ó–°£¨◊Ó–°√ʪ˝Œ™
±£¨Àƒ±þ–ŒPDCQµƒ√ʪ˝◊Ó–°£¨◊Ó–°√ʪ˝Œ™![]() £Æ
£Æ


 «ß¿Ô¬Ì◊þœÚºŸ∆⁄∆⁄ƒ©∑¬’Ê ‘æÌ∫ƺŸœµ¡–¥∞∏
«ß¿Ô¬Ì◊þœÚºŸ∆⁄∆⁄ƒ©∑¬’Ê ‘æÌ∫ƺŸœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨AB£ΩBD£¨°œBAD£Ω50°„£¨°œC£Ω30°„£Æ
(1)«Û°œBACµƒ∂» ˝£ª
(2)»°ADµƒ÷–µ„E£¨¡¨Ω”BE≤¢—”≥§ΩªAC”⁄µ„F£Æ«Û÷§£∫AB£ΩBF£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
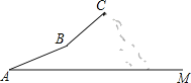
°æƒø°ø Ω҃Ͱ∞ŒÂ“ª°±ºŸ∆⁄£¨ƒ≥Ω×ߪÓ∂Ø–°◊È◊È÷Ø“ª¥Œµ«…ΩªÓ∂Ø£¨À˚√«¥”…ΩΩ≈œ¬Aµ„≥ˆ∑¢—ÿ–±∆¬ABµΩ¥ÔBµ„£¨‘Ÿ¥”Bµ„—ÿ–±∆¬BCµΩ¥Ô…Ω∂•Cµ„£¨¬∑œþ»ÁÕºÀ˘ 棨–±∆¬ABµƒ≥§Œ™200![]() √◊£¨–±∆¬BCµƒ≥§Œ™200
√◊£¨–±∆¬BCµƒ≥§Œ™200![]() √◊£¨∆¬∂» «1£∫1£¨“—÷™Aµ„∫£∞Œ121√◊£¨Cµ„∫£∞Œ721√◊
√◊£¨∆¬∂» «1£∫1£¨“—÷™Aµ„∫£∞Œ121√◊£¨Cµ„∫£∞Œ721√◊
£®1£©«ÛBµ„µƒ∫£∞Œ£ª
£®2£©«Û–±∆¬ABµƒ∆¬∂»£ª
£®3£©Œ™¡À∑Ω±„…œœ¬…Ω£¨»Ù‘⁄AµΩC÷ƺ‰ºÐ…Ë“ªÃı∏÷¿¬£¨«Û∏÷¿¬ACµƒ≥§∂»£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº,≈◊ŒÔœþµƒ∂•µ„Œ™A(-3,-3),¥À≈◊ŒÔœþΩªx÷·”⁄O°¢ B¡Ωµ„.

£®1£©«Û¥À≈◊ŒÔœþµƒΩ‚Œˆ Ω.
£®2£©«Û°˜AOBµƒ√ʪ˝ .
£®3£©»Ù≈◊ŒÔœþ…œ¡Ì”–µ„P¬˙◊„S°˜POB=S°˜AOB,«Î«Û≥ˆP◊¯±Í.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
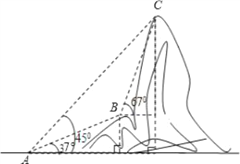
°æƒø°ø»ÁÕº£¨µÁ–≈≤ø√≈º∆ªÆ–ÞΩ®“ªÃı¡¨Ω”B°¢C¡ΩµÿµÁ¿¬£¨≤‚¡ø»À‘±‘⁄…ΩΩ≈A¥¶≤‚µ√B°¢C¡Ω¥¶µƒ—ˆΩ«∑÷± «37°„∫Õ45°„£¨‘⁄B¥¶≤‚µ√C¥¶µƒ—ˆΩ«Œ™67°„£Æ“—÷™Cµÿ±»AµÿÛ{330√◊£®Õº÷–∏˜µ„æ˘‘⁄Õ¨“ª∆Ω√ʃ⁄£©£¨«ÛµÁ¿¬BC≥§÷¡…Ÿ∂ý…Ÿ√◊£ø
£®æ´»∑µΩ√◊£¨≤Œøº ˝æð£∫sin37°„°÷![]() £¨tan37°„°÷
£¨tan37°„°÷![]() £¨sin67°„°÷
£¨sin67°„°÷![]() £¨tan67°„°÷
£¨tan67°„°÷![]() £©
£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Àƒ±þ–Œ![]() ƒ⁄Ω””⁄
ƒ⁄Ω””⁄![]() £¨∂‘Ω«œþ
£¨∂‘Ω«œþ![]() ”⁄
”⁄![]() £¨¡¨Ω”
£¨¡¨Ω”![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() .
.
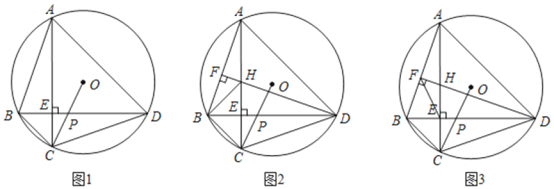
£®1£©»ÁÕº1£¨«Û÷§£∫![]() £ª
£ª
£®2£©»ÁÕº2£¨◊˜![]() ”⁄
”⁄![]() £¨Ωª
£¨Ωª![]() ”⁄
”⁄![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() £ª
£ª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨¡¨Ω”![]() £¨»Ù
£¨»Ù![]() £¨
£¨![]() £¨
£¨![]() ,
,![]() £¨«Û
£¨«Û![]() ≥§.
≥§.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœþ![]() ”Î
”Î![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() ¡Ωµ„(Aµ„‘⁄Bµ„µƒ◊Û±þ)£¨”Î
¡Ωµ„(Aµ„‘⁄Bµ„µƒ◊Û±þ)£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £Æ
£Æ
£®1£©»ÁÕº1£¨»Ù°˜ABCŒ™÷±Ω«»˝Ω«–Œ£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©»ÁÕº1£¨‘⁄£®1£©µƒÃıº˛œ¬£¨µ„![]() ‘⁄≈◊ŒÔœþ…œ£¨µ„
‘⁄≈◊ŒÔœþ…œ£¨µ„![]() ‘⁄≈◊ŒÔœþµƒ∂‘≥∆÷·…œ£¨»Ù“‘
‘⁄≈◊ŒÔœþµƒ∂‘≥∆÷·…œ£¨»Ù“‘![]() Œ™±þ£¨“‘µ„
Œ™±þ£¨“‘µ„![]() °¢
°¢![]() °¢
°¢![]() °¢QŒ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£¨«Û
°¢QŒ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£¨«Û![]() µ„µƒ◊¯±Í£ª
µ„µƒ◊¯±Í£ª
£®3£©»ÁÕº2£¨π˝µ„![]() ◊˜÷±œþ
◊˜÷±œþ![]() µƒ∆Ω––œþΩª≈◊ŒÔœþ”⁄¡Ì“ªµ„
µƒ∆Ω––œþΩª≈◊ŒÔœþ”⁄¡Ì“ªµ„![]() £¨Ωª
£¨Ωª![]() ÷·”⁄µ„
÷·”⁄µ„![]() £¨»Ù
£¨»Ù![]() ©s
©s![]() =1©s4£Æ «Û
=1©s4£Æ «Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨÷±œþy£Ω![]() x+a”Îx÷·Ωª”⁄µ„A£®4£¨0£©£¨”Îy÷·Ωª”⁄µ„B£¨≈◊ŒÔœþy£Ω
x+a”Îx÷·Ωª”⁄µ„A£®4£¨0£©£¨”Îy÷·Ωª”⁄µ„B£¨≈◊ŒÔœþy£Ω![]() x2+bx+cæ≠π˝µ„A£¨B£Æµ„M£®m£¨0£©Œ™x÷·…œ“ª∂ص„£¨π˝µ„M«“¥π÷±”⁄x÷·µƒ÷±œþ∑÷±Ωª÷±œþABº∞≈◊ŒÔœþ”⁄µ„P£¨N£Æ
x2+bx+cæ≠π˝µ„A£¨B£Æµ„M£®m£¨0£©Œ™x÷·…œ“ª∂ص„£¨π˝µ„M«“¥π÷±”⁄x÷·µƒ÷±œþ∑÷±Ωª÷±œþABº∞≈◊ŒÔœþ”⁄µ„P£¨N£Æ
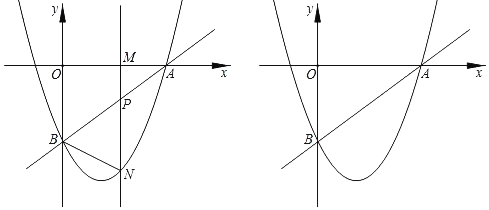
£®1£©ÃÓø’£∫µ„Bµƒ◊¯±ÍŒ™°° °°£¨≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™°° °°£ª
£®2£©µ±µ„M‘⁄œþ∂ŒOA…œ‘À∂Ø ±£®≤ª”ε„O£¨A÷ÿ∫œ£©£¨
¢Ÿµ±mŒ™∫Œ÷µ ±£¨œþ∂ŒPN◊Ó¥Û÷µ£¨≤¢«Û≥ˆPNµƒ◊Ó¥Û÷µ£ª¢⁄«Û≥ˆ π°˜BPNŒ™÷±Ω«»˝Ω«–Œ ±mµƒ÷µ£ª
£®3£©»Ù≈◊ŒÔœþ…œ”–«“÷ª”–»˝∏ˆµ„NµΩ÷±œþABµƒæý¿Î «h£¨«Î÷±Ω”–¥≥ˆ¥À ±”…µ„O£¨B£¨N£¨Pππ≥…µƒÀƒ±þ–Œµƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨“—÷™µ„M£¨Nµƒ◊¯±Í∑÷±Œ™£®©Å2£¨3£©£¨£®3£¨2£©£¨»Ù≈◊ŒÔœþy=ax2©Åx+2£®a°Ÿ0£©”Îœþ∂ŒMN”–¡Ω∏ˆ≤ªÕ¨µƒΩªµ„£¨‘Úaµƒ»°÷µ∑∂Œß «____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com