
����Ŀ��ij��˾����һ�ֽ���Ϊ20Ԫ/���ļ���������������y������������ۼ۸�x��Ԫ/�����ı仯���±���
�۸�x��Ԫ/���� | �� | 30 | 40 | 50 | 60 | �� |
������y������� | �� | 5 | 4 | 3 | 2 | �� |
ͬʱ�����۹����е�������֧���������ۣ��ܼ�40��Ԫ��
��1���۲첢�������е�y��x֮��Ķ�Ӧ��ϵ������ѧ����һ�κ�������������������κ������й�֪ʶд��y���������x��Ԫ/�����ĺ�������ʽ��
��2������ù�˾�������ּ������ľ�������z����Ԫ�������ۼ۸�x��Ԫ/�����ĺ�������ʽ�����ۼ۸�Ϊ����Ԫʱ��������������ֵ�Ƕ��٣�
��3���ù�˾Ҫ�������ܵ���40��Ԫ����д�����ۼ۸�x��Ԫ/������ȡֵ��Χ�������迼�������������ܴ����ۼ۸�Ӧ��Ϊ����Ԫ��
���𰸡��⣺��1�����ݱ��������ݿɵó���y��x��һ�κ�����ϵ�������ʽΪ��y=ax+b��
��![]() ����ã�
����ã� 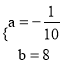 ��
��
����������ʽΪ��y=![]() x+8��
x+8��
��2����������ã�
z=��x��20��y��40=��x��20����![]() x+8����40=
x+8����40=![]() x2+10x��200=
x2+10x��200=![]() ��x2��100x����200
��x2��100x����200
=![]() [��x��50��2��2500]��200=
[��x��50��2��2500]��200=![]() ��x��50��2+50��
��x��50��2+50��
��![]() ��0����x=50��z���=50��
��0����x=50��z���=50��
���ù�˾�������ּ������ľ�������z�����ۼ۸�x���ĺ�������ʽΪz=![]() x2+10x��200�����ۼ۸�Ϊ50Ԫ/��ʱ��������������ֵ��50��Ԫ��
x2+10x��200�����ۼ۸�Ϊ50Ԫ/��ʱ��������������ֵ��50��Ԫ��
��3������˾Ҫ������Ϊ40��Ԫʱ����![]() ��x��50��2+50=40����ã�x1=40��x2=60��
��x��50��2+50=40����ã�x1=40��x2=60��
������ͼ��IJ�ͼ��
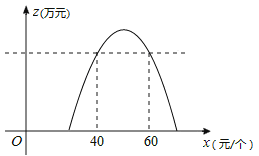
ͨ���۲캯��y=![]() ��x��50��2+50��ͼ��֪���չ�˾Ҫ��ʹ����������40��Ԫ�������ۼ۸��ȡֵ��ΧΪ��40��x��60��
��x��50��2+50��ͼ��֪���չ�˾Ҫ��ʹ����������40��Ԫ�������ۼ۸��ȡֵ��ΧΪ��40��x��60��
��y��x�ĺ�����ϵʽΪ��y=![]() x+8��y��x����������٣�
x+8��y��x����������٣�
�������迼�������������ܴ����ۼ۸�Ӧ��Ϊ40Ԫ/����
�������������������1���������ݵó�y��x��һ�κ�����ϵ���������ô���ϵ������һ�κ�������ʽ��
��2������z=��x��20��y��40�ó�z��x�ĺ�����ϵʽ��Ӧ�ö��κ�����ֵԭ����⼴�ɡ�
��3���������40=![]() ��x��50��2+50ʱx��ֵ���Ӷ����κ��������ʸ��ݵó�x��Ԫ/������ȡֵ��Χ�����һ�κ��������ʼ�����ý����
��x��50��2+50ʱx��ֵ���Ӷ����κ��������ʸ��ݵó�x��Ԫ/������ȡֵ��Χ�����һ�κ��������ʼ�����ý����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���ǣ� ��
A.ͬһ�������Ե�������һ���ǵȻ�
B.������ȵ��������ǵȻ�
C.�������һ������Գ�ͼ��
D.�����ε����ĵ������θ��ߵľ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�͡�ADE�У�AB=AC��AD=AE����BAC+��EAD=180�㣬��ABC��������ADE�Ƶ�A��ת������BE��CD��FΪBE���е㣬����AF��
��1����ͼ�٣�����BAE=90��ʱ����֤��CD=2AF��
��2������BAE��90��ʱ����1���Ľ����Ƿ����������ͼ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB��3��BC��5�����Խ��߽���O��OE��AC��AD��E����AE�ij��ǣ�������
A.1.6
B.2.5
C.3
D.3.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ε����߳��ֱ�Ϊ6��11����ô�����ߵij������ǣ�������
A. 3 B. 4 C. 5 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
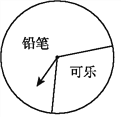
����Ŀ��ij�̳�������һ����������ת����ת��,���涨:�˿���10Ԫ���Ͼ��ܻ��һ��ת��ת�̵Ļ���,��ת��ֹͣʱ,ָ��������һ����Ϳ��Ի����Ӧ�Ľ�Ʒ(��ͼ��ʾ).�±��ǻ�����е�һ��ͳ������:
ת��ת�� �Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1 000 |
������Ǧ���� ����Ĵ���m | 68 | 111 | 136 | 345 | 564 | 701 |
������Ǧ���� �����Ƶ�� |
(1)���㲢��ɱ���.
(2)�����,��n�ܴ�ʱ,������Ǧ���������Ƶ�ʽ���ӽ�����?
(3)������ȥת����ת��һ��,�������ֽ�Ʒ�Ļ����?
(4)�ڸ�ת����,��ʾ��Ǧ������������ε�Բ�Ľ�Լ�Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.3a+2b=5ab
B.5x2y��4x2y=x2y
C.x2+3x3=4x5
D.5x3��2x3=3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com