Question

（1）解不等式：3-x＜2x+6．
（2）分解因式：y³-4y²+4y．
（3）解不等式组：

5x+7＞3(x+1) 1 2 -1≤7- 3 2 x

，并将不等式组的解集在数轴上表示出来．

Answer 1

分析：（1）把不等式的未知项移到不等式左边，常数项移到不等式右边，合并后，把x的系数化为1，即可得到不等式的解集；
（2）原式提取y后，再利用完全平方公式即可化为积的形式；
（3）分别利用去括号及去分母的方法化简不等式组中的两不等式，移项并把x的系数化为1，得到两不等式的解集，把两解集画在数轴上，找出两解集的公共部分，即可得到原不等式组的解集．

解答：解：（1）3-x＜2x+6，
移项得：-x-2x＜6-3，
合并得：-3x＜3，
解得：x＞-1，
则不等式的解集为x＞-1；

（2）y³-4y²+4y
=y（y²-4y+4）
=y（y-2）²；

（3）

5x+7＞3(x+1)① 1 2 -1≤7- 3 2 x②

由①去括号得：5x+7＞3x+3，
移项得：5x-3x＞3-7，
合并得：2x＞-4，
解得：x＞-2，
由②去分母得：1-2≤14-3x，
解得：x≤5，
把两解集画在数轴上，如图所示：

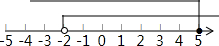
则原不等式组的解集为：-2＜x≤5．

点评：此题考查了一元一次不等式，分解因式以及一元一次不等式组的解法，一元一次不等式常常按照：去分母，去括号，移项，合并，把未知数系数化为1的步骤来求解，而解不等式组既不能“代入”，也不能“加减”，是要分别解不等式组中的每一个不等式，然后借助数轴找出解集的公共部分，从而得到不等式组的解集，熟练以后对于由两个不等式组成的不等式可按“同大取大，同小取小，大大小小无解，大小小大取中间”的规律间接地确定不等式组的解集．