
【题目】如图,正方形ABCD中,E是AB的中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为________°.

【答案】60
【解析】如图,连接DF、BF.如图,连接DF、BF.首先证明∠FDB=![]() ∠FAB=30°,再证明△FAD≌△FBC,推出∠ADF=∠FCB=15°,由此即可解决问题.
∠FAB=30°,再证明△FAD≌△FBC,推出∠ADF=∠FCB=15°,由此即可解决问题.
如图,连接DF、BF.

∵FE⊥AB,AE=EB,∴FA=FB.
∵AF=2AE,∴AF=AB=FB,∴△AFB是等边三角形.
∵AF=AD=AB,∴点A是△DBF的外接圆的圆心,∴∠FDB=![]() ∠FAB=30°.
∠FAB=30°.
∵四边形ABCD是正方形,∴AD=BC,∠DAB=∠ABC=90°,∠ADB=∠DBC=45°,∴∠FAD=∠FBC,∴△FAD≌△FBC,∴∠ADF=∠FCB=15°,∴∠DOC=∠OBC+∠OCB=60°.
故选A.
解法二:连接BF.易知∠FCB=15°,∠DOC=∠OBC+∠FCB=45°+15°=60°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为![]() .如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为
.如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为![]() =3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
=3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)用含t的代数式表示:t秒后,点P表示的数为 ,点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
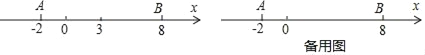
查看答案和解析>>
科目:初中数学 来源: 题型:
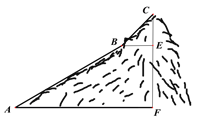
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度![]() ,仰角∠CBE=50°.则山峰的高度CF约为( )米.(可用的参考数据:sin50°≈0.8,tan50°≈1.2,
,仰角∠CBE=50°.则山峰的高度CF约为( )米.(可用的参考数据:sin50°≈0.8,tan50°≈1.2, ![]() )
)
A. 500 B. 518 C. 530 D. 580
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后超过部分按原价85折优惠设顾客预计累计购物![]() 元(
元(![]() )
)
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)某顾客分别到两家超市买了相同的货物,并且所付费用也相同你知道这位顾客共花了多少钱吗?请列出方程解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC.
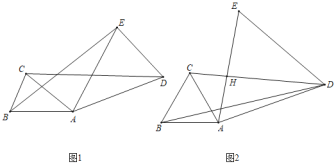
(1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE;
(2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=6,CD=8,求BD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过![]() ,
,![]() 两点.
两点.
(1)求这个一次函数的解析式;
(2)试判断点![]() 是否在这个一次函数的图象上;
是否在这个一次函数的图象上;
(3)求此函数图象与![]() 轴,
轴,![]() 轴围成的三角形的面积.
轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了科学建设“学生健康成长工程”.随机抽取了部分学生家庭对其家长进行了主题为“周末孩子在家您关心吗?”的问卷调查,将回收的问卷进行分析整理,得到了如下的样本统计表和扇形统计图:
代号 | 情况分类 | 家庭数 |
| 带孩子玩并且关心其作业完成情况 | 16 |
| 只关心其作业完成情况 | b |
| 只带孩子玩 | 8 |
| 既不带孩子玩也不关心其作业完成情况 | d |
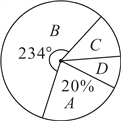
(1)求![]() 的值;
的值;
(2)该校学生家庭总数为500,学校决定按比例在![]() 类家庭中抽取家长组成培训班,其比例为
类家庭中抽取家长组成培训班,其比例为![]() 类取20%,
类取20%,![]() 类各取60%,请你估计该培训班的家庭数;
类各取60%,请你估计该培训班的家庭数;
(3)若在![]() 类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在
类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在![]() 类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,老师在屏幕上出示了一个例题:在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.
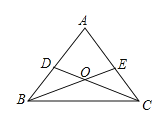
(1)要求同学从这四个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
请你用序号在横线上写出所有情形.答:
(2)选择第(1)题中的一种情形,说明△ABC是等腰三角形的理由,并写出解题过程.
解:我选择 .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
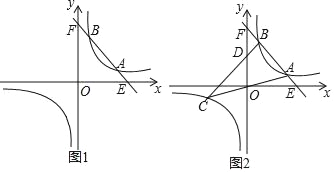
【题目】已知:一次函数y=﹣2x+10的图象与反比例函数y=![]() (k>0)的图象相交于A、B两点(A的B的右侧).
(k>0)的图象相交于A、B两点(A的B的右侧).
(1)当A(4,2)时,求反比例函数的解析式:
(2)当A的横坐标是3,B的横坐标是2时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.
①求C点的坐标;
②求D点的坐标;
③求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com