
【题目】如图,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD. 
(1)求证:△COD是等边三角形.
(2)当α=150°时,试判断△AOD的形状.
(3)探究:当α为多少度时,△AOD是等腰三角形?
【答案】
(1)证明:由旋转的性质知△ADC≌△BOC,
∴DC=OC.
又∵∠DCO=60°,∴△COD是等边三角形
(2)解:∵由旋转的性质知△ADC≌△BOC,
∴α=∠ADC=150°,
∵△COD是等边三角形.
∴∠ODC=60°,
∴∠ADO=90°.
∴△AOD是直角三角形.
(3)解:∠AOD=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∠DAO=180°-(190°-α)-(α-60°)=50°.
若∠ADO=∠AOD,即α-60°=190°-α,∴α=125°;
若∠ADO=∠DAO,即α-60°=50°,∴α=110°;
若∠AOD=∠DAO,即190°-α=50°.∴α=140°.
综上所述,当α=125°或110°或140°时,△AOD是等腰三角形.
【解析】(1)根据旋转的性质得出DC=OC及∠DCO=60°,再根据有一个角是60°的等腰三角形是等边三角形,即可证得结论。
(2)根据旋转的性质得到△ADC≌△BOC,再根据全等三角形的性质求出∠ADC的度数,再根据等边三角形的性质求出∠ODC的度数,然后根据∠ADO=∠ADC-∠ODC,求出∠ADO的度数,就可判断△AOD的形状。
(3)根据旋转的性质分别用含α的式子表示出∠AOD,∠ADO,∠DAO的度数,再分三种情况讨论:∠ADO=∠AOD;∠ADO=∠DAO;∠AOD=∠DAO,计算即可求出满足条件的α的值。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.用一个平面去截一个圆锥,可以是椭圆
B.棱柱的所有侧棱长都相等
C.用一个平面去截一个圆柱体,截面可以是梯形
D.用一个平面去截一个长方体截面不能是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
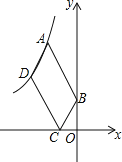
【题目】如图,点A(1-![]() ,1+
,1+![]() )在双曲线
)在双曲线![]() (x<0)上
(x<0)上
(1) 求k的值
(2) 在y轴上取点B(0,1),问双曲线上是否存在点D,使得以AB、AD为斜边的平行四边形ACBD的顶点C在x轴的负半轴上?若存在,求出点D的坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
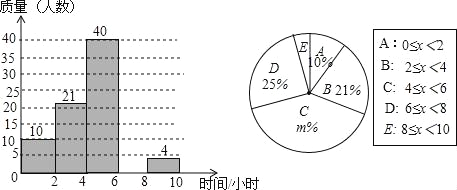
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边△ABC中,AO是BC边上的高,D为AO上一点,以CD为一边,在CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE
(2)过点C作CH⊥BE,交BE的延长线于H,若BC=8,求CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有客房200间供游客居住,当每间客房的定价为每天180元时,客房恰好全部住满;如果每间客房每天的定价每增加10元,就会减少4间客房出租.设每间客房每天的定价增加 ![]() 元,宾馆出租的客房为
元,宾馆出租的客房为 ![]() 间.求:
间.求:
(1)![]() 关于
关于 ![]() 的函数关系式;
的函数关系式;
(2)如果某天宾馆客房收入38400元,那么这天每间客房的价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中学生对待学习的态度一直是教育工作者极为关注的一个问题.为此市教育局对本市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:喜欢;B级:不太喜欢;C级:不喜欢),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了_____名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该市近80000名初中生中大约有多少名学生学习态度达标(达标包括A级和B级)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com