
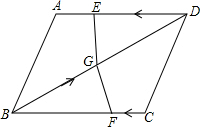
 如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.分析 (1)由AD=BC=12,AB=CD,BD为公共边,所以可证得△ABD≌△CDB,所以可知∠ADB=∠CBD,所以AD∥BC;
(2)设运动时间为t,设G点的移动距离为y,根据全等三角形的性质进行解答即可.
解答 (1)证明:在△ABD和△CDB中,$\left\{\begin{array}{l}{AD=BC}\\{AB=CD}\\{BD=DB}\end{array}\right.$,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,
∴AD∥BC,
(2)解:设G点的移动距离为y,
∵AD∥BC,
∴∠EDG=∠FBG,
若△DEG与△BFG全等,
则有△DEG≌△BFG或△DGE≌△BFG,
可得:DE=BF,DG=BG;或DE=BG,DG=BF,
①当E由D到A,
即0<t≤3时,有4t=12-t,解得:t=2.4,
∵y=15-y,
∴y=7.5,
或4t=y,解得:t=1,
∵12-t=15-y,∴y=4,
②当F由A返回到D,即3<t≤6时,有24-4t=12-t,解得:t=4,
∵y=15-y,∴y=7.5,
或24-4t=y,解得:t=4.2
∵12-t=15-y,y=7.2,
综上可知共有四次,移动的时间分别为1秒、2.4秒、4秒、4.2秒,
移动的距离分别为4、7.5、7.5、7.2.
点评 本题主要考查三角形全等的判定和性质,平行线的判定,根据全等三角形的性质列方程求解,第(2)题解题的关键是利用好三角形全等解得.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 点A、B在数轴上的位置如图所示:
点A、B在数轴上的位置如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 系数是5,次数是n | B. | 系数是-$\frac{5}{8}$,次数是n+1 | ||
| C. | 系数是-$\frac{5}{8}$,次数是n | D. | 系数是-5,次数是n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com