
‘ƒ∂¡œ¬√ʵƒŒƒ◊÷£¨Ω‚¥Œ £Æ
¥Ûº“÷™µ¿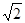 «ŒÞ¿Ì ˝£¨∂¯ŒÞ¿Ì ˝ «ŒÞœÞ≤ª—≠ª∑–° ˝£¨“Ú¥À
«ŒÞ¿Ì ˝£¨∂¯ŒÞ¿Ì ˝ «ŒÞœÞ≤ª—≠ª∑–° ˝£¨“Ú¥À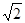 µƒ–° ˝≤ø∑÷Œ“√«≤ªø…ƒÐ»´≤øµÿ–¥≥ˆ¿¥£¨µ´ «”…”⁄1<
µƒ–° ˝≤ø∑÷Œ“√«≤ªø…ƒÐ»´≤øµÿ–¥≥ˆ¿¥£¨µ´ «”…”⁄1<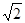 <2£¨À˘“‘
<2£¨À˘“‘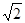 µƒ’˚ ˝≤ø∑÷Œ™1£¨Ω´
µƒ’˚ ˝≤ø∑÷Œ™1£¨Ω´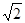 ºı»•∆‰’˚ ˝≤ø∑÷1£¨≤ÓæÕ «–° ˝≤ø∑÷
ºı»•∆‰’˚ ˝≤ø∑÷1£¨≤ÓæÕ «–° ˝≤ø∑÷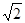 £≠1£¨∏˘æð“‘…œµƒƒ⁄»ð£¨Ω‚¥œ¬√ʵƒŒ £∫
£≠1£¨∏˘æð“‘…œµƒƒ⁄»ð£¨Ω‚¥œ¬√ʵƒŒ £∫
£®1£© µƒ’˚ ˝≤ø∑÷ «_______£¨–° ˝≤ø∑÷ «______£ª
µƒ’˚ ˝≤ø∑÷ «_______£¨–° ˝≤ø∑÷ «______£ª
£®2£©1£´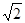 µƒ’˚ ˝≤ø∑÷ «_______£¨–° ˝≤ø∑÷ «____£ª
µƒ’˚ ˝≤ø∑÷ «_______£¨–° ˝≤ø∑÷ «____£ª
£®3£©»Ù…Ë2£´ µƒ’˚ ˝≤ø∑÷ «x£¨–° ˝≤ø∑÷ «y£¨«Ûx£≠
µƒ’˚ ˝≤ø∑÷ «x£¨–° ˝≤ø∑÷ «y£¨«Ûx£≠ yµƒ÷µ
yµƒ÷µ
 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫‘ƒ∂¡¿ÌΩ‚
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 4 |
| 7 |
| 9 |
| 7 |
| 7 |
| 7 |
| 13 |
| 3 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫‘ƒ∂¡¿ÌΩ‚
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫‘ƒ∂¡¿ÌΩ‚
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 4 |
| 7 |
| 9 |
| 7 |
| 7 |
| 7 |
| 5 |
| 13 |
| 5 |
| 3 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫‘ƒ∂¡¿ÌΩ‚
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 11 |
| 11 |
| 11 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫‘ƒ∂¡¿ÌΩ‚
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com