

分析 (1)根据网格中AB所在位置过点C得出直线CQ∥AB即可;
(2)根据网格中点A所在的位置画出AG⊥BC,AH⊥AB即可;
(3)利用点到直线的距离定义得出答案;
(4)由等腰直角三角形的性质得到答案.
解答 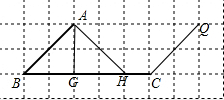 解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:
(3)线段AG的长度是点A到直线BC的距离,线段AH的长度是点H到直线AB的距离;
故答案为:AG,AB;
(4)AG=$\frac{\sqrt{2}}{2}$AH,
理由:∵△AGH是等腰直角三角形,
∠AGH=90°AG=GH,
∵∠AHG=45°,
∴AG=$\frac{\sqrt{2}}{2}$AH.
故答案为:AG=$\frac{\sqrt{2}}{2}$AH,△AGH是等腰直角三角形.
点评 此题主要考查了基本作图以及点到直线的距离等知识,根据题意结合网格各点位置是解题关键.


科目:初中数学 来源: 题型:选择题
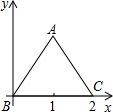 如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )| A. | (1,$\sqrt{3}$) | B. | (1,-$\sqrt{3}$) | C. | (-1,$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:
某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:| x(元) | 60 | 65 | 70 | 75 | … |
| y (件) | 40 | 35 | 30 | 25 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )| A. | $6\sqrt{5}n+5\sqrt{5}$ | B. | $5\sqrt{5}n+\sqrt{5}$ | C. | $6\sqrt{5}n-5\sqrt{5}$ | D. | $5\sqrt{5}n-4\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com