练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．计算$（\frac{1}{m}-1）÷\frac{{1-{m^2}}}{m}$的结果为$\frac{1}{m+1}$．

    分析 先算括号里面的，再算除法即可．

    解答 解：原式=$\frac{1-m}{m}$•$\frac{m}{（1+m）（1-m）}$
    =$\frac{1}{m+1}$．
    故答案为：$\frac{1}{m+1}$．

    点评 本题考查的是分式的混合运算，熟知分式的混合运算，要注意运算顺序，式与数有相同的混合运算顺序；先乘方，再乘除，然后加减，有括号的先算括号里面的是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    19．若两个相似三角形的相似比是1：2，则它们的面积比是1：4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

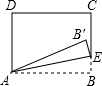    20．如图，在矩形ABCD中，AB=5，BC=3，点E为射线BC上一动点，将△ABE沿AE折叠，得到△AB′E．若B′恰好落在射线CD上，则BE的长为$\frac{5}{3}$或15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．将一副学生用的三角板按如图所示的方式摆放，若AE∥BC，则∠AFD的度数是75°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知，AB是⊙O的直径，AE、AF是弦，BC是⊙O的切线，过点A作AD，使∠DAF=∠AEF．
    （1）如图（1），求证：AD∥BC；
    （2）如图（2），若AD=BC=AB，连接CD，延长AF交CD于G，连接CF，若G为CD中点，求证：CF=CB；
    （3）如图（3），在（2）的条件下，点I在线段FG上，且IF=AF，点P在$\widehat{BE}$上，连接BP并延长到L，使PL=PB，连接AL，延长EA、BI交于点K，已知∠BAK+∠ABL=180°，∠ABI+∠BAL=90°，⊙O的半径为$\frac{{\sqrt{10}}}{2}$，求四边形ALBK的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．若直线y=2x+3b+c与x轴交于点（-2，0），则代数式2-6b-2c的值为-6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

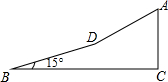    1．如图，某校八年级（1）班学生利用寒假期间到郊区进行社会实践活动，活动之余，同学们准备攀登附近的一个小山坡，从B点出发，沿坡脚15°的坡面以5千米/时的速度行至D点，用了10分钟，然后沿坡比为1：$\sqrt{3}$的坡面以3千米/时的速度达到山顶A点，用了5分钟，求小山坡的高（即AC的长度）（精确到0.01千米）（sin15°≈0.2588，cos15°≈0.9659，$\sqrt{3}$≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图1，等腰直角△ABC和等腰直角△BEF，∠ABC=∠BEF=90°，点F在边BC上，点M为AF的中点，连EM．
    （1）①在图1中画出△BEF关于直线BE成轴对称的三角形；
    ②求证：CF=2ME；
    （2）将图1中的△BEF绕点B逆时针旋转至如图2的位置，其他条件不变，（1）中的结论②是否仍成立？请证明你的结论；
    （3）如图3，过B作BS⊥ME于S，若ES=2，BS=4，CF=10，则S四边形CFEB为40（直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．商场销售某种商品，今年四月份销售了若干件，共获毛利润3万元（每件商品的毛利润=每件商品的销售价格-每件商品的成本价格）．五月份商场在成本价格不变的情况下，把这种商品的每件销售价降低了4元，但销售量比四月增加了500件，从而所获毛利润比四月份增加了2千元．问调价前，销售每件商品的毛利润是多少元？

    查看答案和解析>>

    同步练习册答案