
| n | 3 | 4 | 5 | 6 |
| m | 1 | 0 | 1 | 1 |
| n | 7 | 8 | 9 | 10 |
| m |
| n | 4k-1 | 4k | 4k+1 | 4k+2 |
| m |
分析 探究二:
(1)周长为7,让腰长从1开始逐个验证即可;
(2)周长为8、9、10,方法同上;
解决问题:
问题的本质是,给定三角形的周长n,且n=2a+b,求满足要求的a的整数解的个数m.因此,根据三角形三边关系,我们将a的取值范围用n表示出来,从而就可以确定n在取任意值时,a的整数解个数m;
任意一个整数,均可以表示成4k-1,4k,4k+1,4k+2四种形式当中的一种,让n取这四种值,得出m的值填表;
问题应用:
(1)根据上面探究得出的一般结论,只需看2016符号哪种情况即可.n=2016=504×4,m=504-1=503;
(3)周长相同的情况下,等边三角形面积最大;
解答 解:探究二:
(1)7=1+1+5(舍去);
7=2+2+3(符合要求);
7=3+3+1(符合要求);
(2)8=1+1+6(舍去);
8=2+2+4(舍去);
8=3+3+2(符合要求);
9=1+1+7(舍去);
9=2+2+5(舍去);
9=3+3+3(符合要求);
9=4+4+1(符合要求);
10=1+1+8(舍去);
10=2+2+6(舍去);
10=3+3+4(符合要求);
10=4+4+2(符合要求);
填表如下:
| n | 7 | 8 | 9 | 10 |
| m | 2 | 1 | 2 | 2 |
| n | 4k-1 | 4k | 4k+1 | 4k+2 |
| m | k | k-1 | k | k |
点评 本题以一种探究的方式考查了腰三角形的性质、三角形三边关系、整数解问题,命题新颖,视角独特,是一道经典好题.探究过程中,体现从特殊到一般的归纳思想.掌握好等腰三角形性的基本性质及三角形三边关系是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
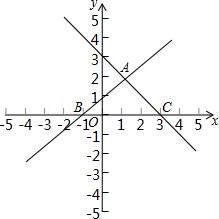 如图,在平面直角坐标系xOy中,直线y=x+1与y=-x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点,在直线AB上存在点E,使得以点E,D,O,A为顶点的四边形是平行四边形,写出$\frac{BE}{CD}$的值.
如图,在平面直角坐标系xOy中,直线y=x+1与y=-x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点,在直线AB上存在点E,使得以点E,D,O,A为顶点的四边形是平行四边形,写出$\frac{BE}{CD}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
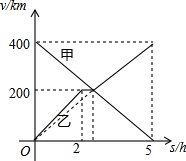 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行.乙车出发2h休息.与甲车相遇.继续行驶.设甲、乙两车与B地的距离y(km)与行驶的时间x(h)之间的函数图象如图所示.
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行.乙车出发2h休息.与甲车相遇.继续行驶.设甲、乙两车与B地的距离y(km)与行驶的时间x(h)之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com