
分析 由a2+5a=-2,b2+2=-5b,即a2+5a+2=0,b2+5b+2=0,且a≠b可知a、b可看做方程x2+5x+2=0的两不相等的实数根,继而知a+b=-5,ab=2,且a<0,b<0,将其代入到原式=-$\frac{b\sqrt{ab}}{a}$-$\frac{a\sqrt{ab}}{b}$=-$\frac{{b}^{2}\sqrt{ab}+{a}^{2}\sqrt{ab}}{ab}$=-$\frac{\sqrt{ab}[(a+b)^{2}-2ab]}{ab}$可得答案.
解答 解:∵a2+5a=-2,b2+2=-5b,即a2+5a+2=0,b2+5b+2=0,且a≠b,
∴a、b可看做方程x2+5x+2=0的两不相等的实数根,
则a+b=-5,ab=2,
∴a<0,b<0,
则原式=-$\frac{b\sqrt{ab}}{a}$-$\frac{a\sqrt{ab}}{b}$
=-$\frac{{b}^{2}\sqrt{ab}+{a}^{2}\sqrt{ab}}{ab}$
=-$\frac{\sqrt{ab}[(a+b)^{2}-2ab]}{ab}$
=-$\frac{\sqrt{2}×(25-4)}{2}$
=-$\frac{21}{2}$$\sqrt{2}$,
故答案为:-$\frac{21}{2}$$\sqrt{2}$.
点评 本题主要考查方程的解、韦达定理、二次根式的化简求值等知识点,根据a、b满足的等式判断出a、b可看做方程x2+5x+2=0的两不相等的实数根且a+b=-5,ab=2,a<0,b<0是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
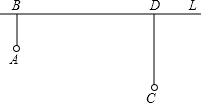 如图,牧童在A处放牛,其家在C处,A、C到河岸L的距离分别为AB=2km,CD=4km且,BD=8km.
如图,牧童在A处放牛,其家在C处,A、C到河岸L的距离分别为AB=2km,CD=4km且,BD=8km.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
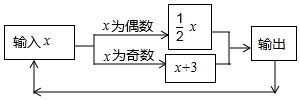 如图所示的运算程序中,若开始输入的x值为-5,我们发现第1次输出的数为-2,再将-2输入,第2次输出的数为-1,如此循环,则第2016次输出的结果为2.
如图所示的运算程序中,若开始输入的x值为-5,我们发现第1次输出的数为-2,再将-2输入,第2次输出的数为-1,如此循环,则第2016次输出的结果为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com