
【题目】某校准备组织师生共60人,从甲地乘动车前往乙地参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
甲地 | 乙地 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)求参加活动的教师和学生各有多少人?
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,后续前往的教师和学生均购买二等座票.设提早前往的教师有![]() 人,购买一、二等座票全部费用为
人,购买一、二等座票全部费用为![]() 元.
元.
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若购买一、二等座票全部费用不多于1030元,则提早前往的教师最多只能有多少人?
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】民间素有“肖县石榴砀山梨,汴梁西瓜红到皮”的谚语,汴梁西瓜是开封的传统特产,驰名古今,畅销中外,某批发商先购买了300千克黑皮无籽西瓜和200千克花皮无籽西瓜,共花费520元,几天后又购买了400千克黑皮无籽西瓜和300千克花皮无籽西瓜,共花费720元(每次两种西瓜的批发价不变),
(1)求黑皮无籽西瓜和花皮无籽西瓜的批发价分别是每千克多少元;
(2)该批发商一段时间后为满足市场需求,还需购买两种西瓜共800千克,要求黑皮无籽西瓜的数量不少于花皮西瓜的3倍,请设计一种购买方案,使所需总费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
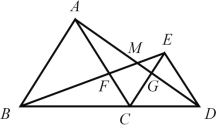
【题目】如图所示,![]() 均为等边三角形,边长分别为
均为等边三角形,边长分别为![]() ,B、C、D三点在同一条直线上,则下列结论正确的________________.(填序号)
,B、C、D三点在同一条直线上,则下列结论正确的________________.(填序号)
①![]() ②
②![]() ③
③![]() 为等边三角形 ④
为等边三角形 ④![]() ⑤CM平分
⑤CM平分![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
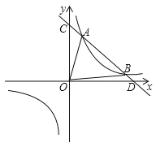
【题目】如图,已知一次函数y1=﹣x+a与x轴、y轴分别交于点D、C两点和反比例函数![]() 交于A、B两点,且点A的坐标是(1,3),点B的坐标是(3,m)
交于A、B两点,且点A的坐标是(1,3),点B的坐标是(3,m)
(1)求a,k,m的值;
(2)求C、D两点的坐标,并求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生产商存有1200千克![]() 产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产
产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产![]() 产品,
产品,![]() 产品售价为200元/千克.经市场调研发现,
产品售价为200元/千克.经市场调研发现,![]() 产品存货的处理价格
产品存货的处理价格![]() (元/千克)与处理数量
(元/千克)与处理数量![]() (千克)满足一次函数关系(
(千克)满足一次函数关系(![]() ),且得到表中数据.
),且得到表中数据.
|
|
200 | 350 |
400 | 300 |
(1)请求出处理价格![]() (元千克)与处理数量
(元千克)与处理数量![]() (千克)之间的函数关系;
(千克)之间的函数关系;
(2)若![]() 产品生产成本为100元千克,
产品生产成本为100元千克,![]() 产品处理数量为多少千克时,生产
产品处理数量为多少千克时,生产![]() 产品数量最多,最多是多少?
产品数量最多,最多是多少?
(3)由于改进技术,![]() 产品的生产成本降低到了
产品的生产成本降低到了![]() 元/千克,设全部产品全部售出,所得总利润为
元/千克,设全部产品全部售出,所得总利润为![]() (元),若
(元),若![]() 时,满足
时,满足![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
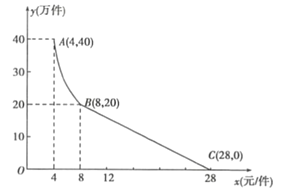
【题目】“净扬”水净化有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的小型水净化产品,已于当年投入生产并进行销售.已知生产这种小型水净化产品的成本为4元/件,在销售过程中发现:每年的年销售量![]() (万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种水净化产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值;
(3)假设公司的这种水净化产品第一年恰好按年利润z(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种水净化产品每件的销售价格x(元)定在8元以上(![]() ),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
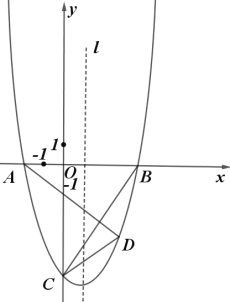
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,
,![]() ,
,![]() ,直线
,直线![]() 是抛物线的对称轴,在直线
是抛物线的对称轴,在直线![]() 右侧的抛物线上有一动点
右侧的抛物线上有一动点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求抛物线的函数表达式;
(2)若点![]() 在
在![]() 轴的下方,当
轴的下方,当![]() 的面积是
的面积是![]() 时,求
时,求![]() 的面积;
的面积;
(3)在(2)的条件下,点![]() 是
是![]() 轴上一点,点
轴上一点,点![]() 是抛物线上一动点,是否存在点
是抛物线上一动点,是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点,以
为顶点,以![]() 为一边的四边形是平行四边形,若存在,求出点
为一边的四边形是平行四边形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
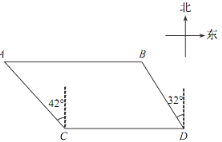
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的木栈道 AB ,栈道 AB 与景区道路CD 平行.在 C 处测得栈道一端 A 位于北偏西 42°方向,在 D 处测得栈道另一端 B 位于北偏西 32°方向.已知 CD =120 m , BD =80 m ,求木栈道 AB 的长度(结果保留整数) .
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com