
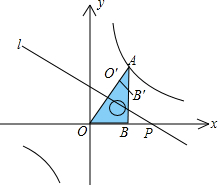
 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y=$\frac{k}{x}$,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是4≤t≤2$\sqrt{5}$或-2$\sqrt{5}$≤t≤-4.
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y=$\frac{k}{x}$,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是4≤t≤2$\sqrt{5}$或-2$\sqrt{5}$≤t≤-4. 分析 当点O′与点A重合时,即点O与点A重合,进一步解直角三角形AOB,利用轴对称求得此时点P的坐标,即t的最小值;然后求出B′在双曲线上时,P的坐标即可.
解答 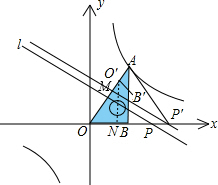 解:当点O′与点A重合时,
解:当点O′与点A重合时,
∵∠AOB=60°,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后是O′B′,AP=OP,
∴△AOP′是等边三角形,
∵B(2,0),
∴BO=BP′=2,
∴点P的坐标是(4,0),
即当P的坐标是(4,0)时,直线O?B?与双曲线有交点O′;
当B′在双曲线上时,作B′C⊥OP于C,
∵BP=B′P,∠B′BP=60°,
∴△BB′P是等边三角形,
∴BP=B′P=t-2,
∴CP=$\frac{1}{2}$(t-2),B′C=$\frac{\sqrt{3}}{2}$(t-2),
∴OC=OP-CP=$\frac{1}{2}$t+1,
∴B′的坐标是($\frac{1}{2}$t+1,$\frac{\sqrt{3}}{2}$(t-2)),
∵∠ABO=90°,∠AOB=60°,OB=2,
∴OA=4,AB=2$\sqrt{3}$,
∴A(2,2$\sqrt{3}$),
∵A和B′都在双曲线上,
∴($\frac{1}{2}$t+1)•$\frac{\sqrt{3}}{2}$(t-2))=2×2$\sqrt{3}$,
解得:t=±2$\sqrt{5}$,
∴t的取值范围是4≤t≤2$\sqrt{5}$或-2$\sqrt{5}$≤t≤-4.
故答案为:4≤t≤2$\sqrt{5}$或-2$\sqrt{5}$≤t≤-4.
点评 本题主要考查对用待定系数法求一次函数、反比例函数的解析式,勾股定理,解二元一次方程组,解不等式,含30度角的直角三角形的性质,三角形的内角和定理,根的判别式等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键,此题是一个拔高的题目,有一定的难度.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
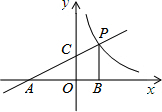 如图,直线$y=\frac{1}{2}x+2$分别交x轴、y轴于A、C两点,且与双曲线$y=\frac{k}{x}$在第一象限交于点P,作PB⊥x轴于B,S△ABP=9.
如图,直线$y=\frac{1}{2}x+2$分别交x轴、y轴于A、C两点,且与双曲线$y=\frac{k}{x}$在第一象限交于点P,作PB⊥x轴于B,S△ABP=9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
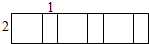 如图是由长方形和正方形从左到右逐个交替并连而成,每个正方形边长为2,每个长方形长为2,宽为1,观察图形,
如图是由长方形和正方形从左到右逐个交替并连而成,每个正方形边长为2,每个长方形长为2,宽为1,观察图形,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com