
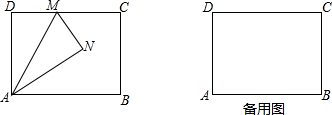
分析 (1)由折叠性质得∠MAN=∠DAM,证出∠DAM=∠MAN=∠NAB,由三角函数得出DM=AD•tan∠DAM=$\sqrt{3}$即可;
(2)延长MN交AB延长线于点Q,由矩形的性质得出∠DMA=∠MAQ,由折叠性质得出∠DMA=∠AMQ,AN=AD=3,MN=MD=1,得出∠MAQ=∠AMQ,证出MQ=AQ,设NQ=x,则AQ=MQ=1+x,证出∠ANQ=90°,在Rt△ANQ中,由勾股定理得出方程,解方程求出NQ=4,AQ=5,即可求出△ABN的面积;
(3)过点A作AH⊥BF于点H,证明△ABH∽△BFC,得出对应边成比例$\frac{BH}{AH}$=$\frac{CF}{BC}$,得出当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,由折叠性质得:AD=AH,由AAS证明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出结果.
解答 解:(1)由折叠性质得:△ANM≌△ADM,
∴∠MAN=∠DAM,
∵AN平分∠MAB,∠MAN=∠NAB,
∴∠DAM=∠MAN=∠NAB,
∵四边形ABCD是矩形,
∴∠DAB=90°,
∴∠DAM=30°,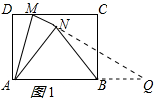
∴DM=AD•tan∠DAM=3×tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$;
(2)延长MN交AB延长线于点Q,如图1所示:
∵四边形ABCD是矩形,
∴AB∥DC,
∴∠DMA=∠MAQ,
由折叠性质得:△ANM≌△ADM,
∴∠DMA=∠AMQ,AN=AD=3,MN=MD=1,
∴∠MAQ=∠AMQ,
∴MQ=AQ,
设NQ=x,则AQ=MQ=1+x,
∵∠ANM=90°,
∴∠ANQ=90°,
在Rt△ANQ中,由勾股定理得:AQ2=AN2+NQ2,
∴(x+1)2=32+x2,
解得:x=4,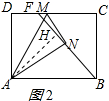
∴NQ=4,AQ=5,
∵AB=4,AQ=5,
∴S△NAB=$\frac{4}{5}$S△NAQ=$\frac{4}{5}$×$\frac{1}{2}$AN•NQ=$\frac{4}{5}$×$\frac{1}{2}$×3×4=$\frac{24}{5}$;
(3)过点A作AH⊥BF于点H,如图2所示:
∵四边形ABCD是矩形,
∴AB∥DC,
∴∠HBA=∠BFC,
∵∠AHB=∠BCF=90°,
∴△ABH∽△BFC,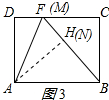
∴$\frac{BH}{AH}$=$\frac{CF}{BC}$,
∵AH≤AN=3,AB=4,
∴当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图3所示:
由折叠性质得:AD=AH,
∵AD=BC,
∴AH=BC,
在△ABH和△BFC中,$\left\{\begin{array}{l}{∠HBA=∠BFC}\\{∠AHB=∠BCF}\\{AH=BC}\end{array}\right.$,
∴△ABH≌△BFC(AAS),
∴CF=BH,
由勾股定理得:BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
∴CF=$\sqrt{7}$,
∴DF的最大值=DC-CF=4-$\sqrt{7}$.
点评 本题考查了矩形的性质、折叠的性质、相似三角形的判定与性质、全等三角形的判定与性质、勾股定理等知识;本题综合性强,难度较大,熟练掌握矩形和折叠的性质,证明三角形相似和三角形全等是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,在4×4的正方形网格中,已有四个小正方形被涂黑.若将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形,则该小正方形的位置可以是( )
如图,在4×4的正方形网格中,已有四个小正方形被涂黑.若将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形,则该小正方形的位置可以是( )| A. | (一,2) | B. | (二,4) | C. | (三,2) | D. | (四,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | 当x1<x2时,y1>y2 | D. | 当x1<x2时,y1<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.
如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
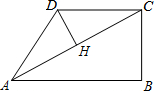 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )| A. | 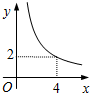 | B. | 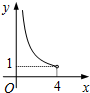 | C. | 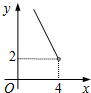 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为10$\sqrt{3}$+1m(结果保留根号).
如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为10$\sqrt{3}$+1m(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E,F,延长BD至G,使得DG=BD,连结EG,FG,若AE=DE,则$\frac{EG}{AB}$=$\frac{\sqrt{7}}{2}$.
如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E,F,延长BD至G,使得DG=BD,连结EG,FG,若AE=DE,则$\frac{EG}{AB}$=$\frac{\sqrt{7}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com