练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

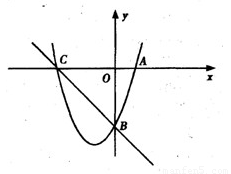
    已知抛物线y=－x2+2(m－3)x+m－1与x轴交于B,A两点,其中点B在x轴的负半轴上,点A在x轴的正半轴上,该抛物线与y轴于点C。
    (1)写出抛物线的开口方向与点C的坐标(用含m的式子表示)；(2分)
    (2)若tg∠CBA=3,试求抛物线的解析式；(6分)
    (3)设点P(x,y)（其中0＜x＜3）是(2)中抛物线上的一个动点,试求四边形AOCP的面积的最大值及此时点P的坐标。(6分)

    （1）抛物线的开口向下,点C的坐标是(0,m－1)（2）y=－x2+2x+3（3）点P的坐标为()时,四边形AOCP的面积达到最大值 

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （9分）如图，已知抛物线y＝x2＋bx－3a过点A(1，0)，B(0，－3)，与x轴交于另一点C．

    (1)求抛物线的解析式；
    (2)若在第三象限的抛物线上存在点P，使△PBC为以点B为直角顶点的直角三角形，
    求点P的坐标；
    (3)在(2)的条件下，在抛物线上是否存在一点Q，使以P，Q，B，C为顶点的四边形
    为直角梯形？若存在，请求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2011届云南省昭通市高中（中专）招生统一模拟考试数学试卷（3）（带解析） 题型：解答题

    如图，已知抛物线y=－x2+2x+3交x轴于A、B两点（点A在点B的左侧），与y轴交于点C。
    （1）求点A、B、C的坐标。
    （2）若点M为抛物线的顶点，连接BC、CM、BM，求△BCM的面积。
    （3）连接AC，在x轴上是否存在点P使△ACP为等腰三角形，若存在，请求出点P的坐标；若不存在，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源：2012年初中毕业升学考试（广东河源卷）数学（解析版） 题型：解答题

    (1)已知方程x2＋px＋q＝0(p2－4q≥0)的两根为x1、x2，求证：x1＋x2＝－p，x1·x2＝q．(2)已知抛物线y＝x2＋px＋q与x轴交于点A、B，且过点(―1，―1)，设线段AB的长为d，当p为何值时，d2取得最小值并求出该最小值．

     

    查看答案和解析>>

    科目：初中数学 来源：2012届苏州工业园区九年级下学期学科调研数学卷 题型：解答题

    （9分）如图，已知抛物线y＝x2＋bx－3a过点A(1，0)，B(0，－3)，与x轴交于另一点C．

        (1)求抛物线的解析式；

        (2)若在第三象限的抛物线上存在点P，使△PBC为以点B为直角顶点的直角三角形，

    求点P的坐标；

        (3)在(2)的条件下，在抛物线上是否存在一点Q，使以P，Q，B，C为顶点的四边形

    为直角梯形？若存在，请求出点Q的坐标；若不存在，请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源：2011年湖北省九年级二次函数单元卷 题型：填空题

    已知抛物线y＝x2－3x－4，则它与x轴的交点坐标是                  .

     

    查看答案和解析>>

    同步练习册答案