
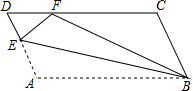
 如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处.若△FDE的周长为6,平行四边形ABCD的周长为26,那么CF的长为7.
如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处.若△FDE的周长为6,平行四边形ABCD的周长为26,那么CF的长为7.  习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
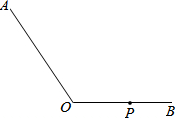 作图并填空:如图,在∠AOB中,点P在边OB上,
作图并填空:如图,在∠AOB中,点P在边OB上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
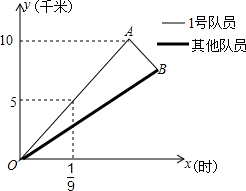 自行车队点的一次训练中,1号队员以高于其他队员10千米/时的速度独自前行,匀速行进一段时间后,又返回队伍,在往返过程中速度保持不变,设分开后行进的时间为x小时,1号队员和其他队员行进的路程分别为y1、y2(千米),且y1、y2与x的函数关系如图所示.
自行车队点的一次训练中,1号队员以高于其他队员10千米/时的速度独自前行,匀速行进一段时间后,又返回队伍,在往返过程中速度保持不变,设分开后行进的时间为x小时,1号队员和其他队员行进的路程分别为y1、y2(千米),且y1、y2与x的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,5) | B. | (3,5) | C. | (3,-3) | D. | (-1,-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com