
【题目】如图,把一个量角器与一块30°(∠CAB=30°)角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有射线CP绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB重合,就停止旋转.在旋转过程中,射线CP与量角器的半圆弧交于E.连接BE.
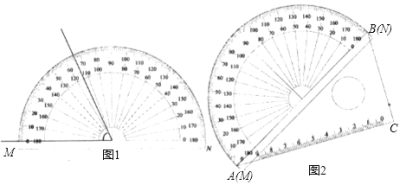
(1)设旋转x秒后,点E处的读数为y°,则y与x的函数关系式________.
(2)当CP旋转________秒时,△BCE是等腰三角形.
【答案】(1)y=4x(0≤x≤45);(2)7.5或30
【解析】
(1)由题意∠ACE=2x°,∠AOE=y°,根据圆周角定理可知∠AOE=2∠ACE,可得y=4x(0≤x≤45);
(2)分两种情形分别讨论求解即可,①如图,当BE=EC时,则有EO垂直平分BC,先根据平行线的性质求出∠AOE=∠BAC=30°,再利用圆周角定理得出∠ACE的度数,从而可得出结果;②当BC=BE时,则有OB垂直平分EC,先判定△BOE是等边三角形,再求出∠AOE的度数,再利用圆周角定理得出∠ACE的度数,从而可得出结果.
解:(1)如图,由题意知∠ACE=2x°,∠AOE=y°,
又∠ACB=90°,∴点C在以O为圆心,AB为直径的圆上,
又MN=AB,∴点C也在以MN为直径的圆上,
∴∠AOE=2∠ACE=4x°,
故答案为:y=4x(0≤x≤45);
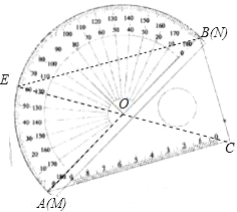
(2)①如图,当BE=EC时,
连接OC,则OB=OC,又EB=EC,
∴EO垂直平分BC,

∵AC⊥BC,∴EO∥AC,
∴∠AOE=∠BAC=30°,
∴∠ACE=![]() ∠AOE=15°,
∠AOE=15°,
t=15÷2=7.5(秒).
②如图,当BC=BE时,
连接OC,则OE=OC,又BC=BE,
∴OB垂直平分EC,
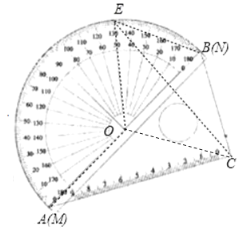
∴∠OBE=∠OBC=60°,
又OE=OB,
∴△BOE是等边三角形,
∴∠AOE=120°,
∴∠ACE=![]() ∠AOE=60°,
∠AOE=60°,
∴t=60÷2=30(秒).
综上可知,当CP旋转7.5秒或30秒时,△BCE是等腰三角形.
故答案为:7.5或30.


科目:初中数学 来源: 题型:
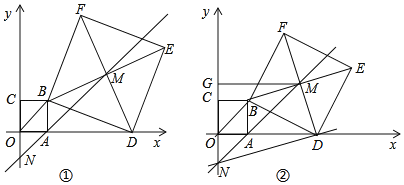
【题目】如图①,在直角坐标系中,点A的坐标为(1,0),以OA为边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形;
(2)试说明(1)中找出的损矩形的四个顶点一定在同一个圆上;
(3)随着点D位置的变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由;
(4)在图②中,过点M作MG⊥y轴于点G,连接DN,若四边形DMGN为损矩形,求D点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具专柜从太原市小商品批发市场购进一批胶带,每个进价0.5元.调查发现,当销售价为0.8元时,每月可售出500个;如果售价每降低0.05元,那么平均每月可多售出200个.
(1)当降价0.2元时,平均每月销售胶带______个;
(2)摊主要想平均每月赢利180元,且尽可能让利与顾客,应该如何定价?
(3)在(2)的条件下,每个胶带的利润率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
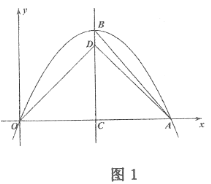
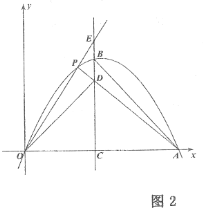
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,对称轴分别交抛物线和
,对称轴分别交抛物线和![]() 轴于点
轴于点![]() 和点
和点![]() ,以
,以![]() 为底边向上作等腰
为底边向上作等腰![]() .
.
(1)![]() ______;
______;![]() ______(用含
______(用含![]() 的代数式表示);
的代数式表示);
(2)如图1,当![]() 时,连接
时,连接![]() ,求
,求![]() 的值;
的值;
(3)点![]() 是抛物线
是抛物线![]() 段上任意一点,连接
段上任意一点,连接![]() 和
和![]() ,延长
,延长![]() 交对称轴于点
交对称轴于点![]() ,如图2,若
,如图2,若![]() ,
,![]() ,
,![]() 三点在一条直线上,当
三点在一条直线上,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是抛物线![]() 对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.
对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至北京时间2020年3月26日11:30,全球新冠肺炎确诊病例突破47万例,已有60个国家宣布进入紧急状态,国外较多医护人员不得不重复使用一次性口罩和防护装备.深圳海王星辰福田某药店购进A、B两种一次性口罩共1500个,已知购进A种一次性口罩和B种一次性口罩的费用分别为3000元和2000元,且A种一次性口罩的单价比B种一次性口罩单价多1元,求A、B两种一次性口罩的单价各是多少?设A种一次性口罩单价为x元,根据题意,列方程正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年2月22日深圳地铁10号线华南城站试运行,预计今年6月正式开通.在地铁的建设中,某段轨道的铺设若由甲乙两工程队合做,12天可以完成,共需工程费用27720元;已知乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
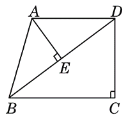
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)若 AD=25,BC=32,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
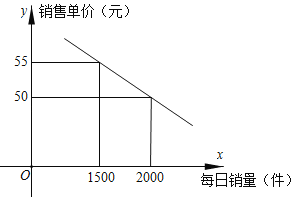
【题目】为倡导节能环保,降低能源消耗,提倡环保型新能源开发,造福社会.某公司研发生产一种新型智能环保节能灯,成本为每件40元.市场调查发现,该智能环保节能灯每件售价y(元)与每天的销售量为x(件)的关系如图,为推广新产品,公司要求每天的销售量不少于1000件,每件利润不低于5元.
(1)求每件销售单价y(元)与每天的销售量为x(件)的函数关系式并直接写出自变量x的取值范围;
(2)设该公司日销售利润为P元,求每天的最大销售利润是多少元?
(3)在试销售过程中,受国家政策扶持,毎销售一件该智能环保节能灯国家给予公司补贴m(m≤40)元.在获得国家每件m元补贴后,公司的日销售利润随日销售量的增大而增大,则m的取值范围是 (直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com