
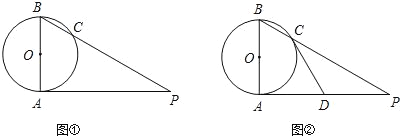
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,求∠ABP的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
【答案】(1)55°;(2)证明见解析.
【解析】
(1)首先根据切线的性质判定∠BAP=90,然后利用直角三角形两锐角互余求出∠ABP;
(2)连接OC、OD、AC,证出∠OCD=90即可,由AB是直径,得到直角三角形ACP,根据直角三角形斜边上的中线等于斜边的一半得到CD=AD,从而△OAD≌△OCD,得到结论.
(1)解:∵AB是⊙O的直径,AP是⊙O的切线,
∴AB⊥AP,
∴∠BAP=90°;
又∵∠P=35°,
∴∠ABP=90°﹣35°=55°.
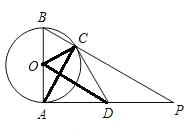
(2)证明:如图,连接OC,OD、AC.
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),
∴∠ACP=90°;
又∵D为AP的中点,
∴AD=CD(直角三角形斜边上的中线等于斜边的一半);
在△OAD和△OCD中,
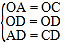 ,
,
∴△OAD≌△OCD(SSS),
∴∠OAD=∠OCD(全等三角形的对应角相等);
又∵AP是⊙O的切线,A是切点,
∴AB⊥AP,
∴∠OAD=90°,
∴∠OCD=90°,即直线CD是⊙O的切线.
故答案为:(1)55°;(2)证明见解析.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
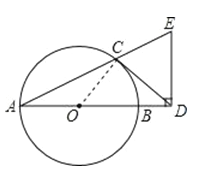
【题目】如图,AB 是⊙O 的直径,CD 与⊙O 相切于点 C,与 AB 的延长线交于点 D,DE⊥AD 且与AC 的延长线交于点 E.
(1)求证:DC=DE;
(2)若 AD=2ED,AB=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题:在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了。有一种用“因式分解”法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() ,此时可以得到数字密码171920.
,此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个).
分解因式后可以形成哪些数字密码?(写出三个).
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为![]() ,求出一个由多项式
,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可).
分解因式后得到的密码(只需一个即可).
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为2434,求
时可以得到其中一个密码为2434,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
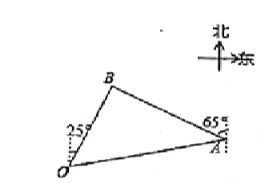
【题目】中国海军亚丁湾护航十年,中国海军被亚丁湾上来往的各国商船誉为“值得信赖的保护伞”.如图,在一次护航行动中,我国海军监测到一批可疑快艇正快速向护航的船队靠近,为保证船队安全,我国海军迅速派出甲、乙两架直升机分别从相距40海里的船队首(![]() 点)尾(
点)尾(![]() 点)前去拦截,8分钟后同时到达
点)前去拦截,8分钟后同时到达![]() 点将可疑快艇驱离.己知甲直升机每小时飞行180海里,航向为北偏东
点将可疑快艇驱离.己知甲直升机每小时飞行180海里,航向为北偏东![]() ,乙直升机的航向为北偏西
,乙直升机的航向为北偏西![]() ,求乙直升机的飞行速度(单位:海里/小时).
,求乙直升机的飞行速度(单位:海里/小时).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村的居民自来水管道需要改造.该工程若由甲队单独施工恰好在规定时间内完成,若乙队单独施工,则完成工程所需天数是规定天数的1.5倍,如果由甲、乙两队先合做![]() 天,那么余下的工程由甲队单独完成还需5天.设这项工程的规定时间是x天,则根据题意,下面所列方程正确的是( )
天,那么余下的工程由甲队单独完成还需5天.设这项工程的规定时间是x天,则根据题意,下面所列方程正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
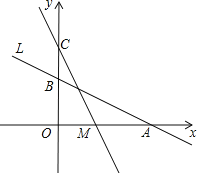
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,请直接写出此时t值和M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
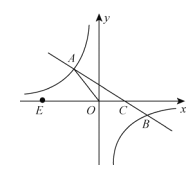
【题目】如图,在平面直角坐标系xoy中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出一次函数值大于反比例函数自变量x的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com