
【题目】某机械租赁公司有同一型号的机械设备40套,经过一段时间的经营发现:当每套机械设备的月租金为270元时,恰好全部租出,在此基础上,当每套设备的月租金提高10元时,这种设备就少租一套,且未租出一套设备每月需要支出费用(维护费、管理费等)20元.
(1)设每套设备的月租金为![]() (元),用含
(元),用含![]() 的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;
的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;
(2)租赁公司的月收益能否达到11040元?此时应该出租多少套机械设备?每套月租金是多少元?请简要说明理由;
(3)租赁公司的月收益能否在11040元基础上再提高?为什么?
【答案】(1)未租出的设备为![]() 套,所有未租出设备的支出费用为
套,所有未租出设备的支出费用为![]() 元;(2)当月租金300元,租出37套;或月租金350元,租出32套,该公司的月收益为11040元,理由见解析;(3)可获得比11040元更高的月收益,理由见解析
元;(2)当月租金300元,租出37套;或月租金350元,租出32套,该公司的月收益为11040元,理由见解析;(3)可获得比11040元更高的月收益,理由见解析
【解析】
(1)设每套设备的月租金为![]() (元),则由题意可得到未租出的设备为
(元),则由题意可得到未租出的设备为![]() 套,进而得到所有未租出设备的支出费用;
套,进而得到所有未租出设备的支出费用;
(2)根据题意,列出方程:![]() ,求解后可得;
,求解后可得;
(3)设月收益为![]() 元,根据题意得到二次函数
元,根据题意得到二次函数![]() ,化为顶点式即可得到答案.
,化为顶点式即可得到答案.
(1)设每套设备的月租金为![]() (元),由题意可得未租出的设备为
(元),由题意可得未租出的设备为![]() (套),
(套),
所有未租出设备的支出费用为:![]() 元;
元;
(2)根据题意,列出方程:![]()
解得![]() ,
,![]()
所以当月租金300元,租出37套;或月租金350元,租出32套,该公司的月收益为11040元;
(3)设月收益为![]() 元,根据题意得,
元,根据题意得,![]()
![]() ,
,
即![]() ,
,
当x=325时,y最大为11102.5,则x为325时,租赁公司出租该型号设备的月收益最大,最大月收益为11102.5元.如果按整10元上调价格,则当x=320或330时,最大收益为11100元,收入也大于11040元.
综上所述,可获得比11040元更高的月收益.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是

A、当弦PB最长时,ΔAPC是等腰三角形 B、当ΔAPC是等腰三角形时,PO⊥AC
C、当PO⊥AC时,∠ACP=300 D、当∠ACP=300时,ΔPBC是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:
(1)体育场离张强家的多远?张强从家到体育场用了多长时间?
(2)体育场离文具店多远?
(3)张强在文具店逗留了多久?
(4)计算张强从文具店回家的平均速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC![]()
![]() ,点E是边AD的中点,连接BE交AC于F,BE的延长线交CD的延长线于G.
,点E是边AD的中点,连接BE交AC于F,BE的延长线交CD的延长线于G.
(1)求证:![]() ;
;
(2)若GE=2,BF=3,求线段EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点,如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动。若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为_____________
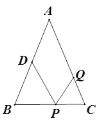
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣![]() x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() 此时可以得到数字密码171920.
此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10m,AD为支柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF等于( )

A.10mB.5mC.2.5mD.9.5m
查看答案和解析>>
科目:初中数学 来源: 题型:
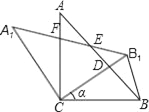
【题目】如图,△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角为ɑ(0°<ɑ<90°),连接BB1.设CB1交AB于点D,A1B1分别交AB、AC于点E,F.
(1)求证:△BCD≌△A1CF;
(2)若旋转角ɑ为30°,
①请你判断△BB1D的形状;
②求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com