
”¾ĢāÄæ”æĪŖĮĖĮĖ½āijĒųµÄĀĢ»Æ½ų³Ģ£¬Š”Ć÷Ķ¬Ń§²éŃÆĮĖŌ°ĮÖĀĢ»ÆÕžĪńĶų£¬øł¾ŻĶųÕ¾·¢²¼µÄ½ü¼øÄźøĆ³ĒŹŠ³ĒŹŠĀĢ»Æ׏Ō“ĒéæöµÄĻą¹ŲŹż¾Ż£¬»ęÖĘĮĖČēĻĀĶ³¼ĘĶ¼£Ø²»ĶźÕū£©
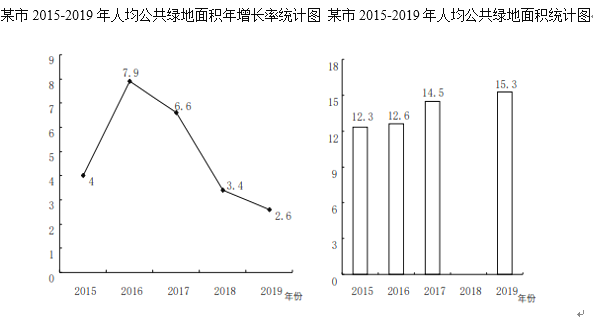
![]() Ēėøł¾ŻŅŌÉĻŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
Ēėøł¾ŻŅŌÉĻŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
![]() Ēó2018ÄźøĆŹŠČĖ¾ł¹«¹²ĀĢµŲĆ껿ŹĒ¶ąÉŁĘ½·½Ć×(¾«Č·µ½
Ēó2018ÄźøĆŹŠČĖ¾ł¹«¹²ĀĢµŲĆ껿ŹĒ¶ąÉŁĘ½·½Ć×(¾«Č·µ½![]() £æ
£æ
![]() ²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
![]() Š”Ć÷Ķ¬Ń§»¹ĮĖ½āµ½×Ō¼ŗÉķ±ßµÄŠķ¶ąĶ¬Ń§¶¼Ź÷Į¢ĘšĮĖĀĢÉ«ĪÄĆ÷ĄķÄī£¬“Ó×ŌÉķ×öĘš£¬¶ąÖÖŹ÷£¬ĪŖĢįøßČĖ¾ł¹«¹²ĀĢµŲĆ껿×ö¹±Ļ×£¬Ėū¶ŌĖłŌŚ°ą¼¶µÄ¶ą
Š”Ć÷Ķ¬Ń§»¹ĮĖ½āµ½×Ō¼ŗÉķ±ßµÄŠķ¶ąĶ¬Ń§¶¼Ź÷Į¢ĘšĮĖĀĢÉ«ĪÄĆ÷ĄķÄī£¬“Ó×ŌÉķ×öĘš£¬¶ąÖÖŹ÷£¬ĪŖĢįøßČĖ¾ł¹«¹²ĀĢµŲĆ껿×ö¹±Ļ×£¬Ėū¶ŌĖłŌŚ°ą¼¶µÄ¶ą![]() ĆūĶ¬Ń§2019Äź²ĪÓėÖ²Ź÷µÄĒéæö×öĮĖµ÷²é£¬²¢øł¾Żµ÷²éĒéæö»ęÖĘ³öČēĻĀĶ³¼Ę±ķ£ŗ
ĆūĶ¬Ń§2019Äź²ĪÓėÖ²Ź÷µÄĒéæö×öĮĖµ÷²é£¬²¢øł¾Żµ÷²éĒéæö»ęÖĘ³öČēĻĀĶ³¼Ę±ķ£ŗ
ÖÖŹ÷æĆŹż£ØæĆ£© |
|
|
|
|
|
|
ČĖŹż |
|
|
|
|
|
|
Čē¹ū°“ÕÕŠ”Ć÷µÄĶ³¼ĘŹż¾Ż£¬ĒėÄćĶعż¼ĘĖć¹Ą¼Ę£¬ĖūĖłŌŚŃ§Š£µÄ![]() ĆūĶ¬Ń§ŌŚ2019Äź¹²Ö²Ź÷¶ąÉŁæĆ£æ
ĆūĶ¬Ń§ŌŚ2019Äź¹²Ö²Ź÷¶ąÉŁæĆ£æ
”¾“š°ø”æ£Ø1£©¢Ł15.0Ę½·½Ć×£»¢Ś¼ū½āĪö£»£Ø2£©675æĆ
”¾½āĪö”æ
£Ø1£©¢Łøł¾ŻĢõŠĪĶ¼æɵĆ2017ÄźøĆŹŠČĖ¾ł¹«¹²ĀĢµŲĆ껿ŹĒ14.5£¬øł¾ŻÕŪĻßĶ¼æÉµĆ³ö2018ÄźøĆ³ĒŹŠČĖ¾ł¹«¹²ĀĢµŲĆ껿ŌŚ2017ÄźµÄ»ł“”ÉĻŌö³¤3.4%£¬½ų¶ųĒó³ö¼“æÉ£»
¢ŚĄūÓĆ¢ŁÖŠĖłĒ󣬻³öĢõŠĪĶ¼¼“æÉ£»
£Ø2£©øł¾Ż40ĆūĶ¬Ń§2019Äź²ĪÓėÖ²Ź÷µÄĒéæö£¬Ēó³öĘ½¾łÖµ£¬¼“æɹĄ¼Ę300ĆūĶ¬Ń§ŌŚ2019Äź¹²Ö²Ź÷æĆŹż£¬
½ā£ŗ£Ø1£©¢Ł14.5”Į£Ø1+3.4%£©”Ö15.0£¬
“š£ŗ2018ÄźøĆŹŠČĖ¾ł¹«¹²ĀĢµŲĆ껿ŹĒ15.0Ę½·½Ć×£»
¢Ś²¹Č«ĢõŠĪĶ³¼ĘĶ¼ČēĻĀ£ŗ
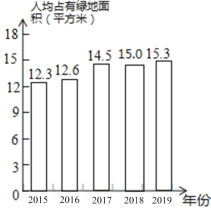
£Ø2£©ĆæČĖĘ½¾łÖ²Ź÷![]() =2.25£ØæĪ£©£¬
=2.25£ØæĪ£©£¬
Ōņ¹Ą¼ĘĖūĖłŌŚŃ§Š£µÄ300ĆūĶ¬Ń§ŌŚ2015Äź¹²Ö²Ź÷300”Į2.25=675æĆ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
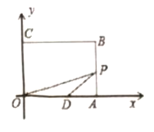
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪ![]() µÄ¶„µć
µÄ¶„µć![]() ·Ö±šŌŚ×ų±źÖįÉĻ£¬
·Ö±šŌŚ×ų±źÖįÉĻ£¬![]() £¬µć
£¬µć![]() ŃŲ
ŃŲ![]() ŌĖ¶Æ£¬Į¬½Ó
ŌĖ¶Æ£¬Į¬½Ó![]() £¬µ±
£¬µ±![]() ĪŖµČŃüČż½ĒŠĪŹ±£¬µć
ĪŖµČŃüČż½ĒŠĪŹ±£¬µć![]() µÄ×ų±źĪŖ__________£®
µÄ×ų±źĪŖ__________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”÷ABC£¬”ĻACB£½90”ć£¬BC£½3£¬AC£½4£¬Š”ŗģ°“ČēĻĀ²½Öč×÷Ķ¼£ŗ
¢Ł·Ö±šŅŌA”¢CĪŖŌ²ŠÄ£¬ŅŌ“óÓŚ![]() ACµÄ³¤ĪŖ°ė¾¶ŌŚACĮ½±ß×÷»”£¬½»ÓŚĮ½µćM”¢N£»
ACµÄ³¤ĪŖ°ė¾¶ŌŚACĮ½±ß×÷»”£¬½»ÓŚĮ½µćM”¢N£»
¢ŚĮ¬½ÓMN£¬·Ö±š½»AB”¢ACÓŚµćD”¢O£»
¢Ū¹żC×÷CE”ĪAB½»MNÓŚµćE£¬Į¬½ÓAE”¢CD£®
ŌņĖıߊĪADCEµÄÖܳ¤ĪŖ£Ø””””£©

A. 10 B. 20 C. 12 D. 24
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗ![]() ÖŠ£¬
ÖŠ£¬![]() £¬ĒóÖ¤£ŗ
£¬ĒóÖ¤£ŗ![]() £¬ĻĀĆꊓ³öæÉŌĖÓĆ·“Ö¤·ØÖ¤Ć÷ÕāøöĆüĢāµÄĖÄøö²½Öč£ŗ
£¬ĻĀĆꊓ³öæÉŌĖÓĆ·“Ö¤·ØÖ¤Ć÷ÕāøöĆüĢāµÄĖÄøö²½Öč£ŗ
¢Ł”ą![]() £¬ÕāÓėČż½ĒŠĪÄŚ½ĒŗĶĪŖ
£¬ÕāÓėČż½ĒŠĪÄŚ½ĒŗĶĪŖ![]() Ƭ¶Ü,¢ŚŅņ“Ė¼ŁÉč²»³ÉĮ¢£®”ą
Ƭ¶Ü,¢ŚŅņ“Ė¼ŁÉč²»³ÉĮ¢£®”ą![]() ,¢Ū¼ŁÉčŌŚ
,¢Ū¼ŁÉčŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() ,¢ÜÓÉ
,¢ÜÓÉ![]() £¬µĆ
£¬µĆ![]() £¬¼“
£¬¼“![]() £®ÕāĖÄøö²½ÖčÕżČ·µÄĖ³ŠņÓ¦ŹĒ£Ø””””£©
£®ÕāĖÄøö²½ÖčÕżČ·µÄĖ³ŠņÓ¦ŹĒ£Ø””””£©
A.¢Ū¢Ü¢Ś¢ŁB.¢Ū¢Ü¢Ł¢ŚC.¢Ł¢Ś¢Ū¢ÜD.¢Ü¢Ū¢Ł¢Ś
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ”ĮśĻŗŃųÖ³“ó»§ĪŖĮĖøüŗƵŲ·¢»Ó¼¼ŹõÓÅŹĘ£¬Ņ»“ĪŠŌŹÕ¹ŗĮĖ20000kgŠ”ĮśĻŗ£¬¼Ę»®ŃųÖ³Ņ»¶ĪŹ±¼äŗóŌŁ³öŹŪ£®ŅŃÖŖĆæĢģ·ÅŃųµÄ·ŃÓĆĻąĶ¬£¬·ÅŃų10ĢģµÄ×ܳɱ¾ĪŖ30.4ĶņŌŖ£»·ÅŃų20ĢģµÄ×ܳɱ¾ĪŖ30.8ĶņŌŖ£Ø×ܳɱ¾=·ÅŃų×Ü·ŃÓĆ+ŹÕ¹ŗ³É±¾£©£®
£Ø1£©ÉčĆæĢģµÄ·ÅŃų·ŃÓĆŹĒaĶņŌŖ£¬ŹÕ¹ŗ³É±¾ĪŖbĶņŌŖ£¬ĒóaŗĶbµÄÖµ£»
£Ø2£©ÉčÕāÅśŠ”ĮśĻŗ·ÅŃųtĢģŗóµÄÖŹĮæĪŖm£Økg£©£¬ĻśŹŪµ„¼ŪĪŖyŌŖ/kg£®øł¾ŻŅŌĶł¾ŃéæÉÖŖ£ŗmÓėtµÄŗÆŹż¹ŲĻµĪŖ![]() £»yÓėtµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
£»yÓėtµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
¢Ł·Ö±šĒó³öµ±0”Üt”Ü50ŗĶ50£¼t”Ü100Ź±£¬yÓėtµÄŗÆŹż¹ŲĻµŹ½£»
¢ŚÉč½«ÕāÅśŠ”ĮśĻŗ·ÅŃųtĢģŗóŅ»“ĪŠŌ³öŹŪĖłµĆĄūČóĪŖWŌŖ£¬Ēóµ±tĪŖŗĪÖµŹ±£¬W×ī“ó£æ²¢Ēó³ö×ī“óÖµ£®£ØĄūČó=ĻśŹŪ×ܶī©×ܳɱ¾£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÄŚ£¬ŅŃÖŖµćAµÄ×ų±źĪŖ£Ø-6£¬0£©£¬Ö±Ļßl£ŗy=kx+b²»¾¹żµŚĖÄĻóĻŽ£¬ĒŅÓėxÖįµÄ¼Š½ĒĪŖ30”ć£¬µćPĪŖÖ±ĻßlÉĻµÄŅ»øö¶Æµć£¬ČōµćPµ½µćAµÄ×ī¶Ģ¾ąĄėŹĒ2£¬ŌņbµÄÖµĪŖ£Ø””””£©
A. ![]() »ņ
»ņ![]() B.
B. ![]() C. 2
C. 2![]() D. 2
D. 2![]() »ņ10
»ņ10![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»Į¾æĶ³µ“Ó¼×µŲ³ö·¢Ē°ĶłŅŅµŲ£¬Ę½¾łĖŁ¶Čv(Ē§Ć×/Š”Ź±)ÓėĖłÓĆŹ±¼ät(Š”Ź±)µÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£¬ĘäÖŠ60”Üv”Ü120.
(1)Ö±½ÓŠ“³övÓėtµÄŗÆŹż¹ŲĻµŹ½£»
(2)ČōŅ»Į¾»õ³µĶ¬Ź±“ÓŅŅµŲ³ö·¢Ē°Ķł¼×µŲ£¬æĶ³µ±Č»õ³µĘ½¾łĆ抔Ź±¶ąŠŠŹ»20Ē§Ć×£¬3Š”Ź±ŗóĮ½³µĻąÓö£®
¢ŁĒóĮ½³µµÄĘ½¾łĖŁ¶Č£»
¢Ś¼×”¢ŅŅĮ½µŲ¼äÓŠĮ½øö¼ÓÓĶÕ¾A”¢B£¬ĖüĆĒĻą¾ą200Ē§Ć×£¬µ±æĶ³µ½ųČėB¼ÓÓĶÕ¾Ź±£¬»õ³µĒ”ŗĆ½ųČėA¼ÓÓĶÕ¾(Į½³µ¼ÓÓĶµÄŹ±¼äŗöĀŌ²»¼Ę)£¬Ēó¼×µŲÓėB¼ÓÓĶÕ¾µÄ¾ąĄė£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
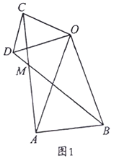
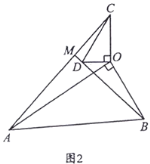
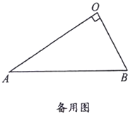
”¾ĢāÄæ”æ£Ø1£©ČēĶ¼1£¬ŌŚ”÷OABŗĶ”÷OCDÖŠ£¬OA=OB£¬OC=OD£¬”ĻAOB=”ĻCOD=50”ć£¬Į¬½ÓAC£¬BD
½»ÓŚµćM£®
¢Ł![]() µÄÖµĪŖ £»¢Ś”ĻAMBµÄ¶ČŹżĪŖ ”ć£»
µÄÖµĪŖ £»¢Ś”ĻAMBµÄ¶ČŹżĪŖ ”ć£»
£Ø2£©ČēĶ¼2£¬ŌŚ”÷OABŗĶ”÷OCDÖŠ£¬”ĻAOB=”ĻCOD=90”ć£¬”ĻOAB=”ĻOCD=30”ć£¬Į¬½ÓAC½»BDµÄŃÓ³¤ĻßÓŚµćM£®Ēó![]() µÄÖµ¼°”ĻAMBµÄ¶ČŹż£»
µÄÖµ¼°”ĻAMBµÄ¶ČŹż£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬½«”÷OCDČʵćOŌŚĘ½ĆęÄŚŠż×Ŗ£¬AC£¬BDĖłŌŚÖ±Ļß½»ÓŚµćM£®ČōOD=![]() £¬OB=
£¬OB=![]() £¬ĒėÖ±½ÓŠ“³öµ±µćCÓėµćMÖŲŗĻŹ±ACµÄ³¤£®
£¬ĒėÖ±½ÓŠ“³öµ±µćCÓėµćMÖŲŗĻŹ±ACµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ°ėŌ²OµÄÖ±¾¶£¬µćPŹĒBAŃÓ³¤ĻßÉĻŅ»µć£¬PCŹĒ”ŃOµÄĒŠĻߣ¬ĒŠµćĪŖC£¬¹żµćB×÷BD”ĶPC½»PCµÄŃÓ³¤ĻßÓŚµćD£¬Į¬½ÓBC£®ĒóÖ¤£ŗ
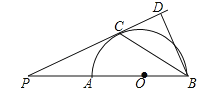
£Ø1£©”ĻPBC=”ĻCBD£»
£Ø2£©![]() =ABBD£®
=ABBD£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com