
【题目】已知:如图,在等边![]() 中,
中,![]() ,且
,且![]() 交
交![]() 外角平分线
外角平分线![]() 于点
于点![]() .
.

(1)当点![]() 为
为![]() 中点时,试说明
中点时,试说明![]() 与
与![]() 的数量关系;
的数量关系;
(2)当点![]() 不是
不是![]() 中点时,试说明
中点时,试说明![]() 与
与![]() 的数量关系.
的数量关系.
【答案】(1)![]() ,见解析.(2)
,见解析.(2)![]() ,见解析.
,见解析.
【解析】
(1)AD=DE.由等边三角形的性质和平行线的性质得到∠BDF=∠BFD=60°,于是得到△BDF是等边三角形,再证明△AFD≌△DCE即可得到结论;
(2)AD=DE.由等边三角形的性质和平行线的性质得到∠BDF=∠BFD=60°,于是得到△BDF是等边三角形,再证明△AFD≌△DCE即可得到结论;
(1)结论:AD=DE,理由如下:
如图: 过点D作DF∥AC,交AB于点F,
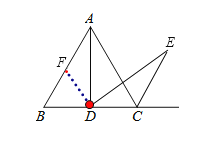
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=∠ABC=60°.
又∵DF∥AC,
∴∠BDF=∠ACB=60°,
∴△BDF是等边三角形,
∴DF=BD,∠BFD=60°,
∵BD=CD,
∴DF=CD
∴∠AFD=120°.
∵EC是外角的平分线,∴∠ACE=60°,
∴∠DCE=∠ACB+∠ACE=120°=∠AFD,
∵∠ADB=∠ADC=90°,
∴∠ADF=∠EDC=30°,
在△AFD与△EDC中,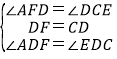 ,
,
∴△AFD≌△DCE(ASA),
∴AD=DE;
(2)结论:AD=DE;理由如下:
如图2,过点D作DF∥AC,交AB于点F,
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=∠ABC=60°,
又∵DF∥AC,
∴∠BDF=∠ACB=60°,
∴△BDF是等边三角形,∴BF=BD,∠BFD=60°,
∴AF=CD,∠AFD=120°,
∵EC是外角的平分线,∴∠ACE=60°,
∴∠DCE=∠ACB+∠ACE=120°=∠AFD,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠FAD=60°+∠FAD,
∵∠ADC=∠ADE+∠EDC=60°+∠EDC,
∴∠FAD=∠EDC,
在△AFD和△DCE中,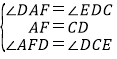 ,
,
∴△AFD≌△DCE(ASA),
∴AD=DE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校团委为积极参与“陶行知杯.全国书法大赛”现场决赛,向学校学生征集书画作品,今年3月份举行了“书画比赛”初赛,初赛成绩评定为A,B,C,D,E五个等级.该校七年级书法班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题.

(1)该校七年级书法班共有 名学生;扇形统计图中C等级所对应扇形的圆心角等于 度,并补全条形统计图;
(2)A等级的4名学生中有2名男生,2名女生,现从中任意选取2名学生参加“陶行知杯.全国书法大赛”现场决赛,请你用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )

A.1B.1.3C.1.2D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,依次连接边长为1的小正方形各边的中点,得到第二个小正方形,再依次连接第二个小正方形各边的中点得到第三个小正方形,按这样的规律第2019个小正方形的面积为
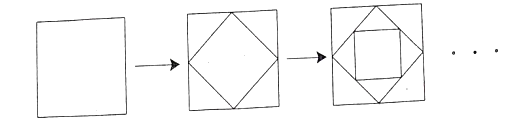
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.观察下面的点阵图和相应的等式,探究其中的规律:
(1)下图反映了任何一个三角形数是如何得到的,认真观察,并在④后面的横线上写出相应的等式;
![]()

(2)通过猜想,写出(1)中与第八个点阵相对应的等式 ;
(3)从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.结合(1)观察下列点阵图,并在⑤看面的横线上写出相应的等式.


(4)通过猜想,写出(3)中与第n个点阵相对应的等式 ;
(5)判断256是不是正方形数,如果不是,说明理由;如果是,256可以看作哪两个相邻的“三角形数”之和?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1,BC=2,点E在AD上,且ED=2AE.
(1)求证:△ABC∽△EAB.
(2)AC与BE交于点H,求HC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2020次“移位”后,他到达编号为______的点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘同学在一次课外活动中,用硬纸片做了两个直角三角形,在![]() 中,
中,![]() ,
,![]() ,
,![]() ;在
;在![]() 中,
中,![]() ,
,![]() ,
,![]() .图①是小刘同学所做的一个数学探究:他将
.图①是小刘同学所做的一个数学探究:他将![]() 的直角边
的直角边![]() 与
与![]() 的斜边
的斜边![]() 重合在一起,并将
重合在一起,并将![]() 沿
沿![]() 方向移动.在移动过程中,
方向移动.在移动过程中,![]() 、
、![]() 两点始终在
两点始终在![]() 边上(移动开始时点
边上(移动开始时点![]() 与点
与点![]() 重合).
重合).
(1)在![]() 沿
沿![]() 方向移动的过程中,小刘发现:
方向移动的过程中,小刘发现:![]() 、
、![]() 两点间的距离逐渐 ;连接
两点间的距离逐渐 ;连接![]() 后,
后,![]() 的度数逐渐 .(填“不变”、“变大”或“变小”);
的度数逐渐 .(填“不变”、“变大”或“变小”);
(2)小刘同学经过进一步地研究,编制了如下问题:
问题①:如图②,当![]() 、
、![]() 的连线与
的连线与![]() 平行时,求平移距离
平行时,求平移距离![]() 的长;
的长;
问题②:如图③,在![]() 的移动过程中,
的移动过程中,![]() 的值是否为定值?如果是,请求出此定值;如果不是,请说明理由.
的值是否为定值?如果是,请求出此定值;如果不是,请说明理由.
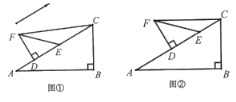

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现:如图1,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上,AE=DG,求证:2S四边形EFGH=S矩形ABCD.(S表示面积)
实验探究:某数学实验小组发现:若图1中AH≠BF,点G在CD上移动时,上述结论会发生变化,分别过点E、G作BC边的平行线,再分别过点F、H作AB边的平行线,四条平行线分别相交于点A1、B1、C1、D1,得到矩形A1B1C1D1.
如图2,当AH>BF时,若将点G向点C靠近(DG>AE),经过探索,发现:2S四边形EFGH=S矩形ABCD+![]() .
.
如图3,当AH>BF时,若将点G向点D靠近(DG<AE),请探索S四边形EFGH、S矩形ABCD与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
迁移应用:
请直接应用“实验探究”中发现的结论解答下列问题:
如图4,点E、F、G、H分别是面积为25的正方形ABCD各边上的点,已知AH>BF,AE>DG,S四边形EFGH=11,HF=![]() ,求EG的长.
,求EG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com