
分析 根据a的取值来确定不等式组的整数解的个数,得知符合题意的只有a=1,再根据等可能概率的公式P(A)=$\frac{m}{n}$求出结论.
解答 解:当a=1时,原不等式组为$\left\{\begin{array}{l}{x>2-1=1}\\{x≤2+2=4}\end{array}\right.$,此时恰有两个整数解x1=3,x2=4;
当a=2时,原不等式组为$\left\{\begin{array}{l}{x>4-1=3}\\{x≤2+2=4}\end{array}\right.$,只有一个整数解x=4;
当a=3时,原不等式组为$\left\{\begin{array}{l}{x>6-1=5}\\{x≤3+2=5}\end{array}\right.$,无解;
当a=4时,原不等式组为$\left\{\begin{array}{l}{x>8-1=7}\\{x≤4+2=6}\end{array}\right.$,无解.
综上可知,使关于x的不等式组$\left\{\begin{array}{l}{x>2a-1}\\{x≤a+2}\end{array}\right.$恰有两个整数解,只有a=1,
取出标有数字1的概率为P=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查了解不等式组与概率公式,解题的关键是根据a的取值来确定不等式组的整数解的个数,得知符合题意的只有a=1.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA.直线y=-$\frac{1}{3}$x+1过点B且与y轴交于点D,E为抛物线顶点.若∠DBC=α,∠CBE=β,
如图,抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA.直线y=-$\frac{1}{3}$x+1过点B且与y轴交于点D,E为抛物线顶点.若∠DBC=α,∠CBE=β,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
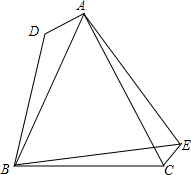 如图,在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转120°-α得到线段BD.
如图,在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转120°-α得到线段BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
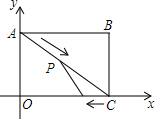 如图,在平面直角坐标系xoy中,四边形OABC是矩形,A(0,6),C(8,0),动点P以每秒2个单位的速度从点A出发,沿AC向点C移动,同时动点Q以每秒1个单位的速度从点C出发,沿CO向点O移动,设P、Q两点移动t秒(0<t<5)后,四边形AOQP的面积为S.
如图,在平面直角坐标系xoy中,四边形OABC是矩形,A(0,6),C(8,0),动点P以每秒2个单位的速度从点A出发,沿AC向点C移动,同时动点Q以每秒1个单位的速度从点C出发,沿CO向点O移动,设P、Q两点移动t秒(0<t<5)后,四边形AOQP的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 无限小数是无理数 | |
| B. | 三角形的外角和等于360° | |
| C. | 相反数等于它本身的数是0和1 | |
| D. | 等边三角形既是中心对称图形,又是轴对称图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
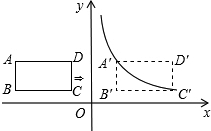 如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2,将矩形ABCD向右平移m个单位,使点A,C恰好同时落在反比例函数y=$\frac{k}{x}$的图象上,得矩形A′B′C′D′,则反比例函数的解析式为y=$\frac{3}{2x}$.
如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2,将矩形ABCD向右平移m个单位,使点A,C恰好同时落在反比例函数y=$\frac{k}{x}$的图象上,得矩形A′B′C′D′,则反比例函数的解析式为y=$\frac{3}{2x}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com