
如图,△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则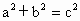 ,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想
,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想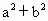 与
与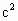 的关系,并证明你的结论.
的关系,并证明你的结论.

|
解:若△ ABC是锐角三角形,则 .若△ABC是钝角三角形,∠C为钝角,则有 .若△ABC是钝角三角形,∠C为钝角,则有 . .
当△ ABC是锐角三角形时,证明如下:如图所示,过点A作AD⊥CB,垂足为D.设CD为x,则有DB=a-x.根据勾股定理,得 . .
即 所以 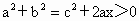 . .
所以 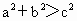 . .
当△ ABC为钝角三角形时,如图所示,过点B作BD⊥AC,交AC的延长线于点D,设CD为x,则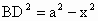 . .
根据勾股定理,得 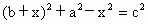 , ,
即 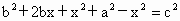 . .
所以  . .
因为 b>0,x>0,所以2bx>0,所以 . .
|
|
要利用勾股定理,必须构造直角三角形,然后在出现的直角三角形中应用勾股定理列出关系式. 在两个直角三角形中,设 CD为x,然后分别用勾股定理表示出等量关系,整理即可. |


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com