
小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的. 规定①玩家只能将小兔从A、B两个出入口放入,②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则应付费3元.
(1)问小美得到小兔玩具的机会有多大?
(2)假设有100人次玩此游戏, 估计游戏设计者可赚多少元?
科目:初中数学 来源: 题型:
阅读理解:如图3,在平面内选一定点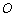 ,引一条有方向的射线
,引一条有方向的射线 ,再选定一个单位长度,那么平面上任一点M的位置可由
,再选定一个单位长度,那么平面上任一点M的位置可由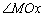 的度数
的度数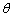 与
与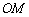 的长度m确定,有序数对(
的长度m确定,有序数对(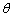 ,m)称为
,m)称为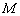 点的“极坐标”,这样建立的坐标系称为“极坐标系”.
点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图4的极坐标系下,如果正六边形的边长为2,有一边OA在射线 上,则正六边形的顶点C的极坐标应记为
上,则正六边形的顶点C的极坐标应记为
A.(60°,4) B.(45°,4) C.(60°,2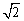 ) D.(50°,2
) D.(50°,2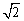 )
)
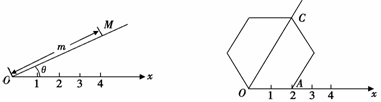
图3  图4
图4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图12, 已知二次函数的图像过点O(0,0), A(4,0),B(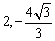 ),M是OA的中点.
),M是OA的中点.
(1)求此二次函数的解析式;
(2)设P是抛物线上的一点,过P作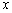 轴的平行线与抛物线交于另一点Q,要使四边形PQAM是菱形,求P点的坐标;
轴的平行线与抛物线交于另一点Q,要使四边形PQAM是菱形,求P点的坐标;
|
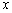 轴下方的部分沿
轴下方的部分沿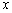 轴向上翻折,得曲线OB′A(B′为B关于
轴向上翻折,得曲线OB′A(B′为B关于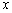 轴的对称点),在原抛物线
轴的对称点),在原抛物线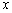 轴的上方部分取一点C,连接CM,CM与翻折后的曲线OB′A交于点D,若△CDA的面积是△MDA面积的2倍,这样的点C是否存在?若存在求出C点的坐标,若不存在,请说明理由.
轴的上方部分取一点C,连接CM,CM与翻折后的曲线OB′A交于点D,若△CDA的面积是△MDA面积的2倍,这样的点C是否存在?若存在求出C点的坐标,若不存在,请说明理由. 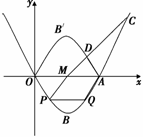
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙、丙、丁四位同学五次数学测验成绩统计如右表所示.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选( )
A.甲 B.乙 C.丙 D.丁
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 | 80 | 85 | 85 | 80 |
| 方 差 | 42 | 42 | 54 | 59 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在“黄袍山国家油茶产业示范园”建设中,某农户计划购买甲、乙两种油茶树苗共1000株.已知乙种树苗比甲种树苗每株贵3元,且用100元钱购买甲种树苗的株数与用160元钱购买乙种树苗的株数刚好相同.
(1)求甲、乙两种油茶树苗每株的价格;
(2)如果购买两种树苗共用5600元,那么甲、乙两种树苗各买了多少株?
(3)调查统计得,甲、乙两种树苗的成活率分别为90%,95%.要使这批树苗的成活率不低于92%,且使购买树苗的费用最低,应如何选购树苗?最低费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com