
【题目】如图1,边长为2的正方形ABCD中,点P在AB边上(不与点A、B重合),点Q在BC边上(不与点B、C重合)
第一次操作:将线段PQ绕点Q顺时针旋转,当点P落在正方形上时,记为点M;
第二次操作:将线段QM绕点M顺时针旋转,当点Q落在正方形上时,记为点N;
依次操作下去…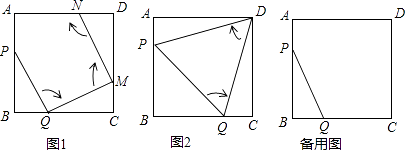
(1)如图2,经过两次操作后得到△PQD、△PQD的形状是 , 求此时线段PQ的长 ;
(2)若经过三次操作可得到四边形PQMN.
①请直接判断四边形PQMN的形状,直接写出此时此刻AP与BQ的数量关系;
②以①中的结论为前提,直接写出四边形PQMN的面积的取值范围.
【答案】
(1)等边三角形,解:由旋转得:DP=PQ=DQ,∴△PQD的形状为等边三角形,∵四边形ABCD是正方形,∴AD=CD=BC=AB,∠A=∠B=∠C=90°,∵DP=DQ,∴Rt△ADP≌Rt△CDQ,∴AP=CQ,∴BP=BQ,∴△BPQ是等腰直角三角形,设BP的长为x,则PQ= ![]() x,∴AP=2﹣x,∵在Rt△ADP中,DP2=AD2+AP2,DP=PQ,∴(
x,∴AP=2﹣x,∵在Rt△ADP中,DP2=AD2+AP2,DP=PQ,∴( ![]() x)2=22+(2﹣x)2,∴x2+4x﹣8=0,解得:x1=﹣2+2
x)2=22+(2﹣x)2,∴x2+4x﹣8=0,解得:x1=﹣2+2 ![]() ,x2=﹣2﹣2
,x2=﹣2﹣2 ![]() (不合题意,舍去),∵PQ=
(不合题意,舍去),∵PQ= ![]() x=
x= ![]() (﹣2+2
(﹣2+2 ![]() )=﹣2
)=﹣2 ![]() +2
+2 ![]() ;
;
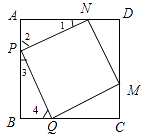
(2)解:①四边形PQMN的形状为正方形,此时AP=BQ.理由如下:
如图所示:
由旋转性质可知,PQ=QM=MN=NP,
∴四边形PQMN是菱形,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
∵∠3+∠4=90°,∠2+∠3=90°,
∴∠QPN=90°,∠2=∠4.
∴四边形PQMN是正方形;
在△APN和△BQP中, 
∴△APN≌△BQP(AAS)
∴AP=BQ.
②利用①中结论得:△APN、△BQP、△CMQ、△DNM均为全等三角形,
∴BQ=CM=DN=AP=x,AN=BP=CQ=DM=2﹣x.
∴四边形PQMN的面积S=S正方形ABCD﹣4S△APN=2×2﹣4× ![]() x(2﹣x)=2x2﹣4x+4,
x(2﹣x)=2x2﹣4x+4,
∴S=2x2﹣4x+4(0<x<2),
∵y=2(x﹣1)2+2,
∴当x=1时,S有最小值2;
当x=0时,S=4,
∴四边形PQMN的面积S取值范围是2≤S<4.
【解析】(1)根据HL证明Rt△ADP≌Rt△CDQ,得AP=CQ,所以△BPQ是等腰直角三角形,设BP的长为x,则PQ= ![]() x,根据勾股定理列方程,解方程即可得PQ的长;(2)①由旋转性质可知,PQ=QM=MN=NP,求出四边形PQMN是菱形,再证出∠QPN=90°,得出四边形PQMN是正方形;由AAS证明△APN≌△BQP,得出AP=BQ即可.②利用①中结论得:△APN、△BQP、△CMQ、△DNM均为全等三角形,得出BQ=CM=DN=AP=x,AN=BP=CQ=DM=2﹣x.四边形PQMN的面积S=S正方形ABCD﹣4S△APN=2x2﹣4x+4,由二次函数的性质即可得出答案.
x,根据勾股定理列方程,解方程即可得PQ的长;(2)①由旋转性质可知,PQ=QM=MN=NP,求出四边形PQMN是菱形,再证出∠QPN=90°,得出四边形PQMN是正方形;由AAS证明△APN≌△BQP,得出AP=BQ即可.②利用①中结论得:△APN、△BQP、△CMQ、△DNM均为全等三角形,得出BQ=CM=DN=AP=x,AN=BP=CQ=DM=2﹣x.四边形PQMN的面积S=S正方形ABCD﹣4S△APN=2x2﹣4x+4,由二次函数的性质即可得出答案.
【考点精析】认真审题,首先需要了解旋转的性质(①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知某的士的起步价为10元(可以坐3千米的路程),若超过3千米,则超出部分每千米另外加收2 元.
(1)小明坐该的士走了x千米的路程,应该付费多少元?
(2)小芳坐该的士走了18千米的路程,应该付费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的身高情况,随机抽取了部分学生的身高进行调查,利用所得数据绘成如下统计图表:
频数分布表
身高分组/cm | 频数 | 百分比 |
| 5 | 10% |
| 20% | |
| 15 | 30% |
| 14 | |
| 6 | 12% |
总计 | 100% |
(1)填空:![]() ______;
______;
(2)通过计算补全频数分布直方图;
(3)该校九年级一共有600名学生,估计身高不低于165cm的学生大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
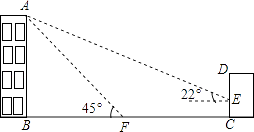
【题目】如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈ ![]() ,cos22°≈
,cos22°≈ ![]() ,tan22°≈
,tan22°≈ ![]() )
) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加某体育训练项目,近期的五次测试成绩得分情况如图.
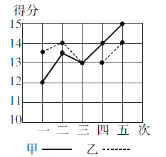
(1)分别求出两人得分的平均数与方差;
(2)根据图和上面算得的结果,对两人的训练成绩作出评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=![]() AB中,一定正确的是( )
AB中,一定正确的是( )
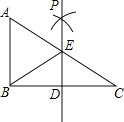
A.①②③ B.①②④ C.①③④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动.(1)设运动时间为t(t>0)秒,数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);(2)若点P、Q同时出发,求:①当点P运动多少秒时,点P与点Q相遇?②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com