
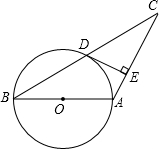
 如图,等腰△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,DE⊥AC于点E.
如图,等腰△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,DE⊥AC于点E.| 5 |
| 5 |
| 5 |
| ||
| 2 |
| OD |
| OE |
5
| ||
| 41 |
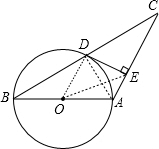 (1)证明:连结OD、AD,如图,
(1)证明:连结OD、AD,如图,| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| AB |
| AD |
| AD |
| AE |
| 5 |
| 5 |
| AD2-AE2 |
| 5 |
| 2 |
| OD2+DE2 |
| ||
| 2 |
| OD |
| OE |
| ||||
|
5
| ||
| 41 |
5
| ||
| 41 |


科目:初中数学 来源: 题型:
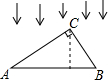 如图,在Rt△ABC中,∠C=90°,投影线方向如图所示,点C在斜边AB上的正投影为点D,
如图,在Rt△ABC中,∠C=90°,投影线方向如图所示,点C在斜边AB上的正投影为点D,查看答案和解析>>
科目:初中数学 来源: 题型:
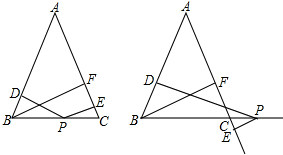
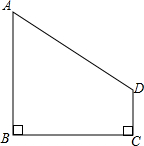 如图,在四边形ABCD中,AB⊥BC,DC⊥BC.当AB=4,DC=1,BC=4时,在BC上是否存在点P,使得AP⊥PD?若存在,求线段BP的长;若不存在,请说明理由.
如图,在四边形ABCD中,AB⊥BC,DC⊥BC.当AB=4,DC=1,BC=4时,在BC上是否存在点P,使得AP⊥PD?若存在,求线段BP的长;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
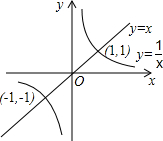 我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙.比如,通过图中的信息我们可以得出x>
我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙.比如,通过图中的信息我们可以得出x>| 1 |
| x |
| A、x>1 |
| B、-1<x<0 |
| C、x>1或-1<x<0 |
| D、以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com