分析:(1)根据反比例函数图象的性质,当比例系数大于0时,函数图象位于第一三象限,列出不等式求解即可;令纵坐标y等于0求出x的值,也就可以得到点A的坐标;
(2)过点M作MC⊥AB于C,根据点A、B的坐标求出AB的长度,再根据S△ABM=8求出MC的长度,然后在Rt△ACM中利用勾股定理求出AC的长度,从而得到OC的长度,也就得到点M的坐标,然后代入反比例函数解析式求出m的值,解析式可得.
解答: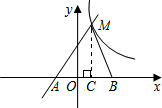
解:(1)∵y=
在第一象限内,
∴m-5>0,
解得m>5,
∵直线y=kx+k与x轴相交于点A,
∴令y=0,
则kx+k=0,
即 k(x+1)=0,
∵k≠0,
∴x+1=0,
解得x=-1,
∴点A的坐标(-1,0);
(2)过点M作MC⊥AB于C,
∵点A的坐标(-1,0)点B的坐标为(3,0),
∴AB=4,AO=1,
S
△ABM=
×AB×MC=
×4×MC=8,
∴MC=4,
又∵AM=5,
∴AC=3,OA=1,
∴OC=2,
∴点M的坐标(2,4),
把M(2,4)代入y=
得
4=
,
解得m=13,
∴y=
.
点评:本题考查了反比例函数图象的性质,一次函数图象的性质,以及勾股定理,待定系数法求函数解析式,综合性较强,但难度不大,审清题意是解题的关键.

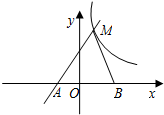 如图,直线y=kx+k(k≠0)与双曲线y=
如图,直线y=kx+k(k≠0)与双曲线y= 解:(1)∵y=
解:(1)∵y=

 名校课堂系列答案
名校课堂系列答案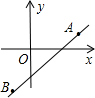 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式