
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:新课程学习手册 数学 八年级(下) 配人教课标版 题型:044
| |||||||
查看答案和解析>>
科目:初中数学 来源:解题升级 解题快速反应一典通 九年级级数学 题型:044
已知抛物线y=x2-(2m+4)x+m2-10与x轴交于A、B两点,C是抛物线的顶点.
(1)用配方法求顶点C的坐标(用含有m的代数式表示);
(2)“若AB的长为2![]() ,求抛物线的解析式”的解法如下:
,求抛物线的解析式”的解法如下:
由(1)知,对称轴与x轴交于点D(________,0).
∵抛物线具有对称性,且AB=2![]() ,
,
∴AD=DB=|xA-xD|=![]() .
.
∵A(xA,0)在抛物线y=(x-h)2+k上,
∴(xA-h)2+k=0. ①
∵h=xC=xD,
∴将|xA-xD|=![]() 代入①,得到关于m的方程0=(
代入①,得到关于m的方程0=(![]() )2+(________). ②
)2+(________). ②
补全解题过程,并简述步骤①的解题依据,步骤②的解题方法.
(3)将(2)中条件“AB的长为2![]() ”改为“△ABC为等边三角形”,用类似的方法求出抛物线的解析式.
”改为“△ABC为等边三角形”,用类似的方法求出抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(浙江台州卷)数学(解析版) 题型:填空题
(1)善于思考的小迪发现:半径为 ,圆心在原点的圆(如图1),如果固定直径
,圆心在原点的圆(如图1),如果固定直径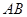 ,把圆内的所有与
,把圆内的所有与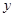 轴平行的弦都压缩到原来的
轴平行的弦都压缩到原来的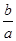 倍,就得到一种新的图形
倍,就得到一种新的图形 椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .
椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .
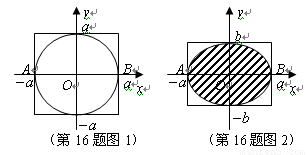
(2)(本小题为选做题,做对另加3分,但全卷满分不超过150分)小迪把图2的椭圆绕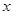 轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为
轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为 的球的体积为
的球的体积为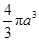 ,则此椭球的体积为 .
,则此椭球的体积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
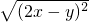 =1,
=1,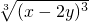 =-1,求
=-1,求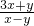 的值.
的值.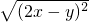 =1,得(2x-y)2=1,2x-y=1第一步
=1,得(2x-y)2=1,2x-y=1第一步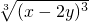 =-1,得x-2y=-1…第二步
=-1,得x-2y=-1…第二步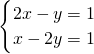 ,解得
,解得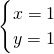 …第三步
…第三步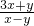 中,得
中,得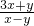 =0 …第四步
=0 …第四步查看答案和解析>>
科目:初中数学 来源:安徽省2011年七年级数学上册一次方程与方程组单元卷 题型:选择题
已知方程组 的解是
的解是 ,则a+b的值为 3 .
,则a+b的值为 3 .
【解析】所谓“方程组”的解,指的是该数值满足方程组中的每一方程.
在求解时,可以将 代入方程
代入方程 得到a和b的关系式,然后求出a,b的值.
得到a和b的关系式,然后求出a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com