
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.

【答案】(1)PM=PN,PM⊥PN,理由见解析;(2)理由见解析;(3)PM=kPN;理由见解析
【解析】试题分析:(1)由等腰直角三角形的性质易证△ACE≌△BCD,由此可得AE=BD,再根据三角形中位线定理即可得到PM=PN,由平行线的性质可得PM⊥PN;(2)(1)中的结论仍旧成立,由(1)中的证明思路即可证明;(3)PM=kPN,由已知条件可证明△BCD∽△ACE,所以可得BD=kAE,因为点P、M、N分别为AD、AB、DE的中点,所以PM=![]() BD,PN=
BD,PN=![]() AE,进而可证明PM=kPN.
AE,进而可证明PM=kPN.
试题解析:(1)PM=PN,PM⊥PN,理由如下:
∵△ACB和△ECD是等腰直角三角形, ∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中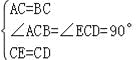 , ∴△ACE≌△BCD(SAS), ∴AE=BD,∠EAC=∠CBD,
, ∴△ACE≌△BCD(SAS), ∴AE=BD,∠EAC=∠CBD,
∵点M、N分别是斜边AB、DE的中点,点P为AD的中点, ∴PM=![]() BD,PN=
BD,PN=![]() AE,
AE,
∴PM=PM, ∵∠NPD=∠EAC,∠MPN=∠BDC,∠EAC+∠BDC=90°, ∴∠MPA+∠NPC=90°,
∴∠MPN=90°, 即PM⊥PN;
(2)∵△ACB和△ECD是等腰直角三角形, ∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE. ∴∠ACE=∠BCD. ∴△ACE≌△BCD. ∴AE=BD,∠CAE=∠CBD.
又∵∠AOC=∠BOE,∠CAE=∠CBD, ∴∠BHO=∠ACO=90°.
∵点P、M、N分别为AD、AB、DE的中点, ∴PM=![]() BD,PM∥BD; PN=
BD,PM∥BD; PN=![]() AE,PN∥AE.
AE,PN∥AE.
∴PM=PN. ∴∠MGE+∠BHA=180°. ∴∠MGE=90°. ∴∠MPN=90°. ∴PM⊥PN.
(3)PM=kPN
∵△ACB和△ECD是直角三角形, ∴∠ACB=∠ECD=90°. ∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD. ∵BC=kAC,CD=kCE, ∴![]() =k. ∴△BCD∽△ACE. ∴BD=kAE.
=k. ∴△BCD∽△ACE. ∴BD=kAE.
∵点P、M、N分别为AD、AB、DE的中点, ∴PM=![]() BD,PN=
BD,PN=![]() AE. ∴PM=kPN.
AE. ∴PM=kPN.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】下列整式乘法运算中,正确的是( )
A.(x-y)(y+ x)=x2-y2 B.(a+3)2=a2+9
C.(a+b)(-a-b)=a2-b2 D.(x-y)2=x2-y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
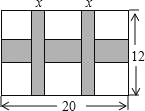
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com