已知抛物线y=-x2+(m-2)x+3(m+1)交x轴于A(x1,0),B(x2,0),交y轴的正半轴于C点,且x1<x2,|x1|>|x2|,OA2+OB2=2OC+1.
(1)求抛物线的解析式;
(2)是否存在与抛物线只有一个公共点C的直线.如果存在,求符合条件的直线的表达式;如果不存在,请说明理由.
【答案】
分析:(1)已知x
1<x
2,|x
1|>|x
2|,很显然,x
1<0,x
2>0,因此OA=-x
1,OB=x
2,然后根据OA
2+OB
2=2OC+1,以及一元二次方程根与系数的关系即可求出m的值.也就可得出函数的解析式.
(2)可根据抛物线的解析式求出C点的坐标,然后分两种情况进行讨论:
①过C的直线与y轴平行(或与x轴垂直),那么此时直线与抛物线只有一个交点.
②如果直线不与y轴平行,可根据C点坐标,设出直线的解析式,然后联立抛物线的解析式可得出一个关于x的一元二次方程,因为两函数只有一个交点,因此方程的△=0,由此可求出直线的解析式.
解答:解:(1)由条件知AO=|x
1|=-x
1,OB=|x
2|=x
2,OC=3(m+1),
∵OA
2+OB
2=2OC+1,x
12+x
22=6(m+1)+1,
∴(x
1+x
2)
2-2x
1x
2=6(m+1)+1,
即(m-2)
2+6(m+1)=6(m+1)+1,
得:m
1=3,m
2=1,
∵x
1<x
2,|x
1|>|x
2|,
∴x
1<x
2=m-2<0,
∴m=1.
∴函数的解析式为y=-x
2-x+6
(2)存在与抛物线只有一个公共点C的直线.
C点的坐标为(0,6),
①当直线过C(0,6)且与x轴垂直时,直线也抛物线只有一个公共点,
∴直线x=0.
②过C点的直线y=kx+6,与抛物线y=x
2-x+6只有一个公共点C,
即
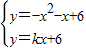
,只有一个实数解.
∴x
2-(k+1)x=0,
又∵△=0,
∴(k+1)
2=0,
∴k=-1,
∴y=-x+6.
∴符合条件的直线的表达式为y=-x+6或x=0.
点评:本题主要考查了一元二次方程根与系数的关系、二次函数解析式的确定以及函数图象交点等知识.

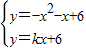 ,只有一个实数解.
,只有一个实数解.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.