练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．如图，计划围一个面积为50m2的长方形场地，一边靠旧墙（墙长为10m），另外三边用篱笆围成，并且它的长与宽之比为5：2．讨论方案时，小英说：“我们不可能围成满足要求的长方形场地．”小军说：“面积和长宽比例是确定的，肯定可以围得出来．”请你判断谁的说法正确，为什么？

    分析 根据矩形的面积公式求出矩形的长和宽，最后进行判断即可得出结论．

    解答 解：设长方形场地的长为5xm，宽为2xm，依题意，得，
    5x•2x=50，
    ∴x=$\sqrt{5}$，
    长为5$\sqrt{5}$，宽为2$\sqrt{5}$．
    ∵4＜5＜9，
    ∴2＜$\sqrt{5}$＜3．
    由上可知2$\sqrt{5}$＜6，且5$\sqrt{5}$＞10
    若长与墙平行，墙长只有10 m，故不能围成满足条件的长方形场地；
    若宽与墙平行，则能围成满足条件的长方形场地．
    ∴他们的说法都不正确．

    点评 此题主要考查了列一元二次方程的应用和解简单的一元二次方程，是一道基础题目，解本题的关键是根据矩形的面积公式建立方程求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届辽宁省九年级3月月考数学试卷（解析版） 题型：填空题

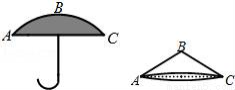
    如图，一把打开的雨伞可近似的看成一个圆锥，伞骨（面料下方能够把面料撑起来的支架）末端各点所在圆的直径AC长为12分米，伞骨AB长为9分米，那么制作这样的一把雨伞至少需要绸布面料为__平方分米．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年贵州省七年级下学期第一次月考数学试卷（解析版） 题型：解答题

    完成正确的证明：如图，已知AB∥CD，求证：∠BED=∠B+∠D

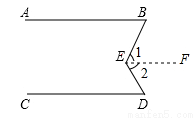
    证明：过E点作EF∥AB（ ）

    ∴∠1= （ ）

    ∵AB∥CD（ ）

    ∴EF∥CD（ ）

    ∴∠2= （ ）

    又∠BED=∠1+∠2

    ∴∠BED=∠B+∠D（ ）．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年贵州省七年级下学期第一次月考数学试卷（解析版） 题型：单选题

    的算术平方根是( )

    A. ±2 B. 2 C. ±4 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．加工某种机器零件，要经过三道工序，第一道工序每名工人每小时可完成6个零件，第二道工序每名工人每小时可完成10个零件，第三道工序每名工人每小时可完成15个零件．要使加工生产均衡，三道工序最少共需要（　　）名工人．
    A．15B．10C．8D．12

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

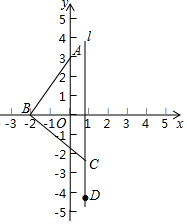    12．如图，已知在平面直角坐标系中，点A（0，3），点B为x轴上一动点，连接AB，线段AB绕着点B按顺时针方向旋转90°至线段CB，过点C作直线l∥y轴，在直线l上有一点D位于点C下方，满足CD=BO，则当点B从（-3，0）平移到（3，0）的过程中，点D的运动路径长为3+3$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．在锐角△ABC中，AB=AC，AD为BC边上的高，E为AC中点．
    （1）如图1，过点C作CF⊥AB于F点，连接EF．若∠BAD=20°，求∠AFE的度数；
    （2）若M为线段BD上的动点（点M与点D不重合），过点C作CN⊥AM于N点，射线EN，AB交于P点．
    ①依题意将图2补全；
    ②小宇通过观察、实验，提出猜想：在点M运动的过程中，始终有∠APE=2∠MAD．
    小宇把这个猜想与同学们进行讨论，形成了证明该猜想的几种想法：
    想法1：连接DE，要证∠APE=2∠MAD，只需证∠PED=2∠MAD．
    想法2：设∠MAD=α，∠DAC=β，只需用α，β表示出∠PEC，通过角度计算得∠APE=2α．
    想法3：在NE上取点Q，使∠NAQ=2∠MAD，要证∠APE=2∠MAD，只需证△NAQ∽△APQ．
    …
    请你参考上面的想法，帮助小宇证明∠APE=2∠MAD．（一种方法即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．在△ABC中，AB=AC，∠ABC=90°，D为AC中点，点P是线段AD上的一点，点P与点A、点D不重合），连接BP．将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P，连接A1B1、BB1
    （1）如图①，当0°＜α＜90°，在α角变化过程中，请证明∠PAA1=∠PBB2．
    （2）如图②，直线AA1与直线PB、直线BB1分别交于点E，F．设∠ABP=β，当90°＜α＜180°时，在α角变化过程中，是否存在△BEF与△AEP全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由；
    （3）如图③，当α=90°时，点E、F与点B重合．直线A1B与直线PB相交于点M，直线BB′与AC相交于点Q．若AB=$\sqrt{2}$，设AP=x，求y关于x的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．在△ABC中，AB=AC，∠A=60°，点D是线段BC的中点，∠EDF=120°，DE与线段AB相交于点E，DF与线段AC（或AC的延长线）相交于点F．
    （1）如图1，若DF⊥AC，垂足为F，AB=8，求BE的长；
    （2）如图2，将（1）中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F．求证：BE+CF=$\frac{1}{2}$AB；
    （3）如图3，将（2）中的∠EDF继续绕点D顺时针旋转一定的角度，使DF与线段AC的延长线相交于点F，作DN⊥AC于点N，若DN=FN，AB=8，求BE的长．

    查看答案和解析>>

    同步练习册答案