
| A. | 3-$\sqrt{2}$ | B. | 3+$\sqrt{2}$ | C. | -3-$\sqrt{2}$ | D. | -3+$\sqrt{2}$ |
分析 由韦达定理可得α+β=-$\sqrt{3}$、αβ=-$\frac{\sqrt{2}}{2}$,代入到α2+β2=(α+β)2-2αβ中计算可得.
解答 解:根据题意得,α+β=-$\frac{\sqrt{6}}{\sqrt{2}}$=-$\sqrt{3}$,αβ=-$\frac{1}{\sqrt{2}}$=-$\frac{\sqrt{2}}{2}$,
则α2+β2=(α+β)2-2αβ
=(-$\sqrt{3}$)2-2×(-$\frac{\sqrt{2}}{2}$)
=3+$\sqrt{2}$.
故选:B.
点评 本题主要考查一元二次方程根与系数的关系,掌握根与系数的关系是根本,待求代数式变形是解题的关键.


科目:初中数学 来源: 题型:选择题
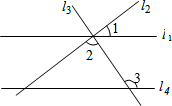 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )| A. | 26° | B. | 36° | C. | 46° | D. | 56° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知一次函数y=ax+c的图象如图所示,那么一元二次方程ax2+bx+c=0的根的情况是( )
已知一次函数y=ax+c的图象如图所示,那么一元二次方程ax2+bx+c=0的根的情况是( )| A. | 方程有两个不相等的实数根 | B. | 方程有两个相等的实数根 | ||
| C. | 方程没有实数根 | D. | 无法判断 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a8÷a4=a2 | B. | a3•a4=a12 | C. | $\sqrt{4}$=±2 | D. | 2x3•x2=2x5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 “瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”的图案中,是轴对称图形的为( )
“瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”的图案中,是轴对称图形的为( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方程无实数根 | B. | 方程有两个相等的实数根 | ||
| C. | 方程有两个不相等的实数根 | D. | 方程的根无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com