
 甲、乙、丙、丁四位同学一起研究一道数学题.如图,已知EF⊥AB,CD⊥AB,
甲、乙、丙、丁四位同学一起研究一道数学题.如图,已知EF⊥AB,CD⊥AB,分析 根据平行线的判定得出CD∥EF,根据平行线的性质得出∠BFE=∠BCD,求出∠CDG=∠BCD,根据平行线的判定得出DG∥BC,即可判断甲;根据∠AGD=∠ACB推出DG∥BC,根据平行线的性质得出∠CDG=∠BCD,即可判断乙,根据已知条件判断丙和丁即可.
解答 解:甲、乙正确;
理由是:∵CD⊥AB,FE⊥AB,
∴CD∥EF,
∴∠BFE=∠BCD,
∵∠CDG=∠BFE,
∴∠CDG=∠BCD,
∴DG∥BC,
∴∠AGD=∠ACB,∴甲正确;
∵CD⊥AB,FE⊥AB,
∴CD∥EF,
∴∠BFE=∠BCD,
∵∠AGD=∠ACB,
∴DG∥BC,
∴∠CDG=∠BCD,
∴∠CDG=∠BFE,∴乙正确;
丙和丁的说法根据已知不能推出,∴丙错误,丁错误;
故答案为:甲、乙.
点评 本题考查了平行线的性质和判定,能灵活运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:解答题
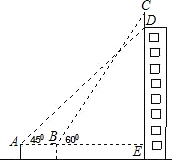 如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)
如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
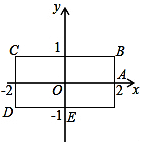 如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是(-1,1).
如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是(-1,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
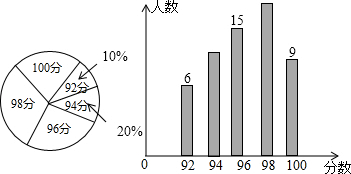
| A. | 94分,96分 | B. | 96分,96分 | C. | 94分,96.4分 | D. | 96分,96.4分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com