
【题目】下列事件中是必然事件的是( )
A. 两弧长相等,则两弧所对圆心角相等
B. 平分弦的直径,也平分这条弦所对的弧
C. 圆内接正五边形的中心角为72°
D. 两圆相切,一定内切
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若一图形各点的纵坐标不变,横坐标分别减5,则图形与原图形相比( )
A. 向右平移了5个单位长度 B. 向左平移了5个单位长度
C. 向上平移了5个单位长度 D. 向下平移了5个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】一节数学课后,老师布置了一道课后练习题:
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.
(1)阅读理解,完成解答
本题证明的思路可用下列框图表示:

根据上述思路,请你完整地书写这道练习题的证明过程;

(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按b元收费,该市小明家今年9、10月份的用水量和所交水费如下表所示:
月份 | 用水量(m3) | 收费(元) |
9 | 5 | 7.5 |
10 | 9 | 18 |
设小明家每月用水量x(立方米),应交水费y(元).
⑴则a= ,b= ;
⑵ 当x≤6,x>6时,分别写出y与x的函数关系式;
⑶ 若该户11月份、12月份用水量为14立方米共交水费27元(11月份用水小于12月份用水),求该户11月份水、12月份用水各多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年春节期间,在网络上用“百度”搜索引擎搜索“开放二孩”,能搜索到与之相关的结果个数约为45100000,这个数用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在离水面高度(AC)为2米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米的速度收绳子.
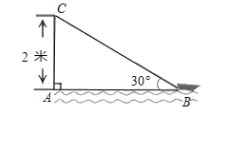
问:(1)未开始收绳子的时候,图中绳子BC的长度是多少米?
(2)收绳2秒后船离岸边多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com