
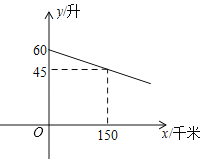
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写出自变量x的取值范围)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,求提示时汽车行驶的路程是多少千米.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
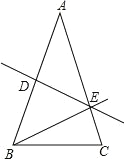
【题目】如图,△ABC是等边三角形,AB=6,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)证明:在运动过程中,点D是线段PQ的中点;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,对于任意两点A (a,b),B(c,d),若点T(x,y)满足x=![]() ,y=
,y=![]() ,那么称点T是点A和B的融合点.例如:M(﹣1,8),N(4,﹣2),则点T(1,2)是点M和N的融合点.如图,已知点D(3,0),点E是直线y=x+2上任意一点,点T (x,y)是点D和E的融合点.
,那么称点T是点A和B的融合点.例如:M(﹣1,8),N(4,﹣2),则点T(1,2)是点M和N的融合点.如图,已知点D(3,0),点E是直线y=x+2上任意一点,点T (x,y)是点D和E的融合点.
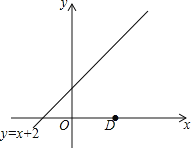
(1)若点E的纵坐标是6,则点T的坐标为 ;
(2)求点T (x,y)的纵坐标y与横坐标x的函数关系式:
(3)若直线ET交x轴于点H,当△DTH为直角三角形时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“黄金1号”玉米种子的价格为5元/kg.如果一次购买5kg以上的种子,超过5kg部分的种子价格打8折.
(1)购买3kg种子,需付款 元,购买6kg种子,需付款 元.
(2)设购买种子x kg,付款金额为y元,写出y与x之间的函数解析式.
(3)张大爷要购买种子5千克,李大爷要购买种子4千克,怎样购买让他们花钱最少?他们各应付款多少元?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系,根据图象,下列信息错误的是( )

A.小明看报用时8分钟
B.公共阅报栏距小明家200米
C.小明离家最远的距离为400米
D.小明从出发到回家共用时16分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB>BC,AB=AC,DE 是 AB 的垂直平分线,垂足为 D,交 AC 于 E.
(1)若∠ABE=40°,求∠EBC 的度数;
(2)若△ABC 的周长为 41cm,一边长为 15cm,求△BCE 的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,且∠FBD=35°,∠BDF=75°,下列说法:①△BDF≌CDE;②ABD和△ACD面积相等;③BF∥CE;④∠DEC=70°,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com