
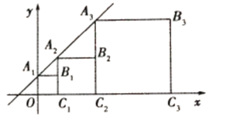
【题目】点![]() 在条直线上,点
在条直线上,点![]() 在
在![]() 轴上,若正方形
轴上,若正方形![]() 按如图所示的位置放置,且
按如图所示的位置放置,且![]() 的面积是1,直线
的面积是1,直线![]() 与
与![]() 轴的夹角是45°,则点
轴的夹角是45°,则点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
首先求出直线![]() 解析式,然后依次找到A2,A3,A4的坐标,得出规律即可找到
解析式,然后依次找到A2,A3,A4的坐标,得出规律即可找到![]() 的坐标.
的坐标.
如图,设直线![]() 与x轴交于点B,
与x轴交于点B,

∵![]() 的面积是1
的面积是1
∴OA1=OC1=1,则A1坐标为(0,1)
∵∠A1BO=45°
∴△A1BO为等腰直角三角形,
∴OB= OA1=1,
则B点坐标为(-1,0),
设直线![]() 解析式
解析式![]() ,将A1,B的坐标代入得
,将A1,B的坐标代入得
![]() ,解得
,解得![]()
∴直线![]() 解析式为
解析式为![]()
∵OC1=1
∴A2的横坐标为1,
将x=1代入![]() ,得
,得![]() ,则A2的坐标为(1,2),
,则A2的坐标为(1,2),
∴A2C1=2= C1C2
则A3的横坐标为1+2=3,同理可得A3的坐标为(3,4),
∴A3C2=4= C2C3
则A4的横坐标为1+2+4=7,同理可得A4的坐标为(7,8),
以此类推,
An的横坐标为1+2+4+…+![]() =
=![]() ,An的坐标(
,An的坐标(![]() ,
,![]() ),
),
可得A2020的横坐标为![]() ,则A2020的坐标为(
,则A2020的坐标为(![]() ,
,![]() ),
),
故选C.


科目:初中数学 来源: 题型:
【题目】某公司拟用运营指数y来量化考核司机的工作业绩,运营指数(y)与运输次数(n)和平均速度(x)之间满足关系式为y=ax2+bnx+100,当n=1,x=30时,y=190;当n=2,x=40时,y=420
用含x和n的式子表示y;
当运输次数定为3次,求获得最大运营指数时的平均速度;
若n=2,x=40,能否在n增加m%(m>0),同时x减少m%的情况下,而y的值保持不变,若能,求出m的值;若不能,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市以20元/千克的进货价购进了一批绿色食品,如果以30元/千克销售这些绿色食品,那么每天可售出400千克.由销售经验可知,每天的销售量y(千克)与销售单价x(元)(x≥30)存在如图所示的一次函数关系.
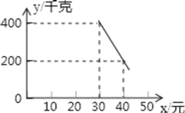
(1)试求出y与x的函数关系式;
(2)设该超市销售该绿色食品每天获得利润w元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李准备进行如下的操作,把一根长![]() 的铁丝剪成两段,并把每段首尾相连各围成一个长宽不等的矩形,两矩形相似且相似比为
的铁丝剪成两段,并把每段首尾相连各围成一个长宽不等的矩形,两矩形相似且相似比为![]() .
.
(1)要使这两个矩形的面积之和为![]() ,较小矩形的长宽各是多少?
,较小矩形的长宽各是多少?
(2)小李认为这两个矩形的面积和不可能为![]() ,你同意吗?说明理由.(说明:相似多边形的周长比等于相似比,面积比等于相似比的平方)
,你同意吗?说明理由.(说明:相似多边形的周长比等于相似比,面积比等于相似比的平方)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并解答问题:杨辉和他的一个数学问题:提起代数,人们自然就和方程联系起米.事实上,我国古代对代数的研究,特别是对方程的解法研究有着优良的传统并取得了重要成果.杨辉,字谦光,钱塘(今浙江杭州)人,南宋杰出的数学家和数学教育家,杨辉一生留下了大量的著述,他著名的数学书共五种二十一卷.下面是杨辉在1275年提出的一个问题(选自杨辉所著《田亩比类乘除算法》):直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.请你用学过的知识解决这个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
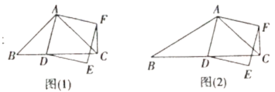
【题目】在![]() 中,
中, ![]() ,点
,点![]() (不与点
(不与点![]() 重合)是线段
重合)是线段![]() 上的一个动点,连接
上的一个动点,连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作正方形
的右侧作正方形![]() ,连接
,连接![]()
(1)发现问题:如图(1),若![]() ,则
,则![]() 与
与![]() 的位置关系_________;
的位置关系_________;
(2)拓展探究:如图(2),若![]() ,(1)中的结论是否仍然成立?请说明理由;
,(1)中的结论是否仍然成立?请说明理由;
(3)解决问题:若![]() ,设正方形
,设正方形![]() 的边
的边![]() 与线段
与线段![]() 相交于点
相交于点![]() ,请直接写出线段
,请直接写出线段![]() 的最大值
的最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,双曲线
,双曲线![]()
![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,且与
,且与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
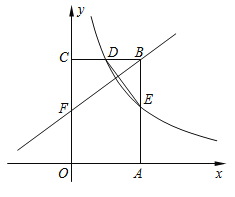
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)若点![]() 是
是![]() 边上一点,且
边上一点,且![]() 相似于
相似于![]() .求直线
.求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在y轴,x轴上,点B的坐标为![]() ,直线
,直线![]() 分别交AB,BC于点M,N,
分别交AB,BC于点M,N,![]() ,反比例函数
,反比例函数![]() 图象经过点M,N.
图象经过点M,N.
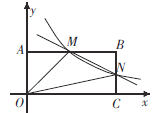
(1)求反比例函数的表达式;
(2)根据图象,请直接写出不等式![]() 的解集________.
的解集________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线y=-x2+2![]() x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+
x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+![]() AP的最小值为( ).
AP的最小值为( ).
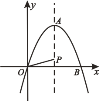
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com