
”¾ĢāÄæ”æij“óѧɜĄūÓĆŹī¼Ł40ĢģÉē»įŹµ¼ł²ĪÓėĮĖŅ»¼ŅĶųµź¾ÓŖ£¬ĮĖ½āµ½Ņ»ÖÖŠĀŠĶÉĢĘ·³É±¾ĪŖ20ŌŖ/¼ž£¬µŚxĢģĻśŹŪĮæĪŖp¼ž£¬ĻśŹŪµ„¼ŪĪŖqŌŖ£¬¾øś×Łµ÷²é·¢ĻÖ£¬Õā40ĢģÖŠpÓėxµÄ¹ŲĻµ±£³Ö²»±ä£¬Ē°20Ģģ£Ø°üŗ¬µŚ20Ģģ£©£¬qÓėxµÄ¹ŲĻµĀś×ć¹ŲĻµŹ½q£½30+ax£»“ÓµŚ21Ģģµ½µŚ40ĢģÖŠ£¬qŹĒ»ł“”¼ŪÓėø”¶Æ¼ŪµÄŗĶ£¬ĘäÖŠ»ł“”¼Ū±£³Ö²»±ä£¬ø”¶Æ¼ŪÓėx³É·“±Č£®ĒŅµĆµ½ĮĖ±ķÖŠµÄŹż¾Ż£®
X£ØĢģ£© | 10 | 21 | 35 |
q£ØŌŖ/¼ž£© | 35 | 45 | 35 |
£Ø1£©ĒėÖ±½ÓŠ“³öaµÄÖµĪŖ”” ””£»
£Ø2£©“ÓµŚ21Ģģµ½µŚ40ĢģÖŠ£¬ĒóqÓėxĀś×ćµÄ¹ŲĻµŹ½£»
£Ø3£©ČōøĆĶųµźµŚxĢģ»ńµĆµÄĄūČóyŌŖ£¬²¢ĒŅŅŃÖŖÕā40ĢģĄļĒ°20ĢģÖŠyÓėxµÄŗÆŹż¹ŲĻµŹ½ĪŖy£½©![]() x2+15x+500
x2+15x+500
iĒėÖ±½ÓŠ“³öÕā40ĢģÖŠpÓėxµÄ¹ŲĻµŹ½ĪŖ£ŗ”” ””£»
iiĒóÕā40ĢģĄļøĆĶųµźµŚ¼øĢģ»ńµĆµÄĄūČó×ī“ó£æ
”¾“š°ø”æ£Ø1£©0.5£»£Ø2£©![]() £»£Ø3£©i£ŗ q£½50©x£»ii£ŗÕā40ĢģĄļøĆĶųµźµŚ21Ģģ»ńµĆµÄĄūČó×ī“ó
£»£Ø3£©i£ŗ q£½50©x£»ii£ŗÕā40ĢģĄļøĆĶųµźµŚ21Ģģ»ńµĆµÄĄūČó×ī“ó
”¾½āĪö”æ
£Ø1£©ĄūÓƱķøńÖŠµÄŹżÖµ“śČėæɵĆaµÄÖµ£»
£Ø2£©øł¾ŻŅŃÖŖÉč![]() £¬ĄūÓƱķøńµÄĮ½øöµćµÄ×ų±ź“śČėæÉµĆ½āĪöŹ½£»
£¬ĄūÓƱķøńµÄĮ½øöµćµÄ×ų±ź“śČėæÉµĆ½āĪöŹ½£»
£Ø3£©i£¬øł¾Żµ±1”Üx”Ü20Ź±£¬ĄūÓĆyµÄ¹ŲĻµŹ½æɵĆpµÄ¹ŲĻµŹ½£»ii£¬·Ö±š¼ĘĖćĒ°20ĢģŗĶŗó20ĄūČóµÄ×ī“óÖµ£¬Č»ŗó±Č½ĻĮ½ÕߵēóŠ”æÉµĆ½įĀŪ£®
£Ø1£©ÓɱķøńæÉÖŖ£ŗµ±x£½10Ź±£¬q£½35£¬
“śČėq£½30+axÖŠµĆ£ŗ35£½30+10a£¬a£½0.5£¬
¹Ź“š°øĪŖ£ŗ0.5£»
£Ø2£©Éč“ÓµŚ21Ģģµ½µŚ40ĢģÖŠ£¬qÓėxĀś×ćµÄ¹ŲĻµŹ½£ŗ![]() £¬
£¬
°Ń£Ø21£¬45£©ŗĶ£Ø35£¬35£©“śČėµĆ£ŗ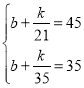 £¬
£¬
½āµĆ£ŗ![]() £¬
£¬
”ąq£½20+![]() £»
£»
£Ø3£©i£¬Ē°20Ģģ£Ø°üŗ¬µŚ20Ģģ£©£ŗy£½©![]() x2+15x+500£½p£Øq©20£©£½p£Ø30+0.5x©20£©£¬
x2+15x+500£½p£Øq©20£©£½p£Ø30+0.5x©20£©£¬
x2©30x©1000£½p£Ø©x©20£©£¬
£Øx©50£©£Øx+20£©£½p£Ø©x©20£©£¬
p£½50©x£¬
¹Ź“š°øĪŖ£ŗq£½50©x£»
ii£¬µ±1”Üx”Ü20Ź±£¬y£½©![]() x2+15x+500£½©
x2+15x+500£½©![]() £Øx©15£©2+612.5£¬
£Øx©15£©2+612.5£¬
µ±x£½15Ź±£¬yÓŠ×ī“óÖµŹĒ612.5£»
µ±21”Üx”Ü40Ź±£¬y£½£Ø50©x£©£Ø20+![]() ©20£©£½
©20£©£½![]() ©525£¬
©525£¬
”ßyĖęxµÄŌö“ó¶ų¼õŠ”£¬
”ąµ±x£½21Ź±£¬yÓŠ×ī“óÖµ£¬ŹĒ725£¬
×ŪÉĻĖłŹö£¬Õā40ĢģĄļøĆĶųµźµŚ21Ģģ»ńµĆµÄĄūČó×ī“ó£®


 ĒÉѧĒÉĮ·ĻµĮŠ“š°ø
ĒÉѧĒÉĮ·ĻµĮŠ“š°ø æĪæĪĮ·½ĖÕĻµĮŠ“š°ø
æĪæĪĮ·½ĖÕĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÕż·½ŠĪABCDÖŠ£¬µćE£¬F½«¶Ō½ĒĻßACČżµČ·Ö£¬ĒŅAC£½9£¬µćPŌŚÕż·½ŠĪµÄ±ßÉĻ£¬ŌņĀś×ćPE+PF£½8µÄµćPµÄøöŹżŹĒ£Ø””””£©
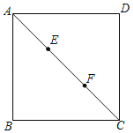
A.8B.6C.4D.0
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¾ÅÄź¼¶Ņ»°ąŃūĒė![]() ”¢
Ӣ![]() Ӣ
Ӣ![]() Ӣ
Ӣ![]() Ӣ
”¢![]() ĪåĪ»ĘĄĪƶŌ¼×”¢ŅŅĮ½Ī»Ķ¬Ń§µÄ²ÅŅÕ±ķŃŻ“ņ·Ö£¬²¢×éÖÆČ«°ą50ĆūĶ¬Ń§¶ŌĮ½ČĖĆńŅā²āĘĄĶ¶Ę±£¬»ęÖĘĮĖČēĻĀµÄ“ņ·Ö±ķŗĶ²»ĶźÕūµÄĢõŠĪĶ³¼ĘĶ¼£ŗ
ĪåĪ»ĘĄĪƶŌ¼×”¢ŅŅĮ½Ī»Ķ¬Ń§µÄ²ÅŅÕ±ķŃŻ“ņ·Ö£¬²¢×éÖÆČ«°ą50ĆūĶ¬Ń§¶ŌĮ½ČĖĆńŅā²āĘĄĶ¶Ę±£¬»ęÖĘĮĖČēĻĀµÄ“ņ·Ö±ķŗĶ²»ĶźÕūµÄĢõŠĪĶ³¼ĘĶ¼£ŗ
ĪåĪ»ĘĄĪƵēņ·Ö±ķ
A | B | C | D | E | |
¼× | 89 | 91 | 93 | 94 | 86 |
ŅŅ | 88 | 87 | 90 | 98 | 92 |
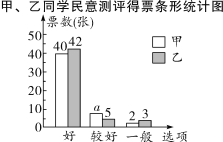
²¢ĒóµĆĮĖĪåĪ»ĘĄĪƶŌ¼×Ķ¬Ń§²ÅŅÕ±ķŃŻĖł“ņ·ÖŹżµÄĘ½¾ł·ÖŗĶÖŠĪ»Źż£ŗ
![]() £Ø·Ö£©£»ÖŠĪ»ŹżŹĒ91·Ö.
£Ø·Ö£©£»ÖŠĪ»ŹżŹĒ91·Ö.
£Ø1£©ĒóĪåĪ»ĘĄĪƶŌŅŅĶ¬Ń§²ÅŅÕ±ķŃŻĖł“ņ·ÖŹżµÄĘ½¾ł·ÖŗĶÖŠĪ»Źż£»
£Ø2£©![]() ________£¬²¢²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
________£¬²¢²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
£Ø3£©ĪŖĮĖ“Ó¼×”¢ŅŅĮ½ČĖ֊ֻє°Ī³öŅ»ČĖČ„²Ī¼ÓŅÕŹõ½ŚŃŻ³ö£¬°ą¼¶ÖʶØĮĖČēĻĀµÄŃ”°Ī¹ęŌņ£ŗ
Ń”°Ī¹ęŌņ£ŗŃ”°Ī×ŪŗĻ·Ö×īøßµÄĶ¬Ń§²Ī¼ÓŅÕŹõ½ŚŃŻ³ö.ĘäÖŠ£¬×ŪŗĻ·Ö£½²ÅŅÕ·Ö![]() ²āĘĄ·Ö
²āĘĄ·Ö![]() £»
£»
²ÅŅÕ·Ö£½ĪåĪ»ĘĄĪÆĖł“ņ·ÖŹżÖŠČ„µōŅ»øö×īøß·ÖŗĶŅ»øö×īµĶ·Ö£¬ŌŁĖćĘ½¾ł·Ö£»²āĘĄ·Ö£½”°ŗĆ”±Ę±Źż”Į2·Ö£«”°½ĻŗĆ”±Ę±Źż”Į1·Ö£«”°Ņ»°ć”±Ę±Źż”Į0·Ö
¢Łµ±![]() Ź±£¬Ķعż¼ĘĖćĖµĆ÷Ӧє°ĪÄÄĪ»Ķ¬Ń§Č„²Ī¼ÓŅÕŹõ½ŚŃŻ³ö£æ
Ź±£¬Ķعż¼ĘĖćĖµĆ÷Ӧє°ĪÄÄĪ»Ķ¬Ń§Č„²Ī¼ÓŅÕŹõ½ŚŃŻ³ö£æ
¢ŚĶعż¼ĘĖćĖµĆ÷![]() µÄÖµ²»ÄÜŹĒ¶ąÉŁ£æ
µÄÖµ²»ÄÜŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½«Õż·½ŠĪ![]() µÄ±ß
µÄ±ß![]() Čʵć
Čʵć![]() ÄꏱÕėŠż×ŖÖĮ
ÄꏱÕėŠż×ŖÖĮ![]() £¬¼ĒŠż×Ŗ½ĒĪŖ
£¬¼ĒŠż×Ŗ½ĒĪŖ![]() £®Į¬½Ó
£®Į¬½Ó![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() “¹Ö±ÓŚÖ±Ļß
“¹Ö±ÓŚÖ±Ļß![]() £¬“¹×ćĪŖµć
£¬“¹×ćĪŖµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬
£¬
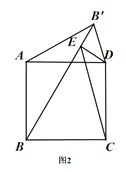
![]() ČēĶ¼1£¬µ±
ČēĶ¼1£¬µ±![]() Ź±£¬
Ź±£¬![]() µÄŠĪדĪŖ £¬Į¬½Ó
µÄŠĪדĪŖ £¬Į¬½Ó![]() £¬æÉĒó³ö
£¬æÉĒó³ö![]() µÄÖµĪŖ £»
µÄÖµĪŖ £»

![]() µ±
µ±![]() ĒŅ
ĒŅ![]() Ź±£¬
Ź±£¬
¢Ł![]() ÖŠµÄĮ½øö½įĀŪŹĒ·ńČŌČ»³ÉĮ¢?Čē¹ū³ÉĮ¢£¬Ēė½ö¾ĶĶ¼2µÄĒéŠĪ½ųŠŠÖ¤Ć÷£»Čē¹ū²»³ÉĮ¢£¬ĒėĖµĆ÷ĄķÓÉ£»
ÖŠµÄĮ½øö½įĀŪŹĒ·ńČŌČ»³ÉĮ¢?Čē¹ū³ÉĮ¢£¬Ēė½ö¾ĶĶ¼2µÄĒéŠĪ½ųŠŠÖ¤Ć÷£»Čē¹ū²»³ÉĮ¢£¬ĒėĖµĆ÷ĄķÓÉ£»
¢Śµ±ŅŌµć![]() ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪŹ±£¬ĒėÖ±½ÓŠ“³ö
ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪŹ±£¬ĒėÖ±½ÓŠ“³ö![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijµŲŅ»ÖÖÉĢĘ·µÄŠčĒóĮæ![]() £ØĶņ¼ž£©ÓėÉĢĘ·¼Ūøń
£ØĶņ¼ž£©ÓėÉĢĘ·¼Ūøń![]() £ØŌŖ/¼ž£©“ęŌŚŅ»“ĪŗÆŹż¹ŲĻµ£¬ĒŅ¼ŪøńĪŖ10ŌŖ/¼žŹ±£¬ŠčĒóĮæŹĒ50Ķņ¼ž£»µ±¼ŪøńŹĒ20ŌŖ/¼žŹ±£¬ŠčĒóĮæŹĒ40Ķņ¼ž£¬øĆÉĢĘ·µÄ¹©Ó¦Įæ
£ØŌŖ/¼ž£©“ęŌŚŅ»“ĪŗÆŹż¹ŲĻµ£¬ĒŅ¼ŪøńĪŖ10ŌŖ/¼žŹ±£¬ŠčĒóĮæŹĒ50Ķņ¼ž£»µ±¼ŪøńŹĒ20ŌŖ/¼žŹ±£¬ŠčĒóĮæŹĒ40Ķņ¼ž£¬øĆÉĢĘ·µÄ¹©Ó¦Įæ![]() £ØĶņ¼ž£©ÓėÉĢĘ·µÄ¼Ūøń
£ØĶņ¼ž£©ÓėÉĢĘ·µÄ¼Ūøń![]() £ØŌŖ/¼ž£©µÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
£ØŌŖ/¼ž£©µÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
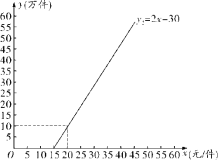
£Ø1£©Ēó![]() ¹ŲÓŚ
¹ŲÓŚ![]() µÄŗÆŹż¹ŲĻµŹ½£¬²¢ŌŚ×ų±źĻµÖŠ»³öĖüµÄĶ¼Ļó£»
µÄŗÆŹż¹ŲĻµŹ½£¬²¢ŌŚ×ų±źĻµÖŠ»³öĖüµÄĶ¼Ļó£»
£Ø2£©ŅŖŹ¹ÉĢĘ·¼ŪøńĻą¶ŌĪČ¶Ø£¬Šč±£³Ö¹©Ó¦ĮæÓėŠčĒóĮæµÄ“óÖĀĘ½ŗā£Ø¼ņ³Ę¹©ŠčĘ½ŗā£©£¬ÄćČĻĪŖÉĢĘ·µÄ¼Ūøń¶ØŌŚĆ漞¶ąÉŁŌŖŹ±£¬¹©Šč×īĘ½ŗā£»ÉĢĘ·¼ŪøńŹĒĆ漞¶ąÉŁŌŖŹ±£¬¹©“óÓŚĒó£æ
£Ø3£©µ±ŹŠ³”¹©Ó¦Įæ“óÓŚŠčĒóĮæµÄ![]() Ź±£¬Õžø®¾Ķ»į·¢³öŌ¤¾Æ£¬ÄĒĆ“Õžø®·¢³öŌ¤¾ÆŹ±£¬ÉĢĘ·µÄ×īµĶ¼ŪøńŹĒĆ漞¶ąÉŁŌŖ£æ£Ø¾«Č·µ½ŌŖ£©
Ź±£¬Õžø®¾Ķ»į·¢³öŌ¤¾Æ£¬ÄĒĆ“Õžø®·¢³öŌ¤¾ÆŹ±£¬ÉĢĘ·µÄ×īµĶ¼ŪøńŹĒĆ漞¶ąÉŁŌŖ£æ£Ø¾«Č·µ½ŌŖ£©
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com