
(2005 海南)如图所示,抛物线 与x轴交于A(-1,0)、B(3,0)两点.
与x轴交于A(-1,0)、B(3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足 ,并求出此时P点的坐标;
,并求出此时P点的坐标;
(3)设(1)中的抛物线交y轴于C点.在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
|
解 (1)抛物线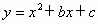 与x轴的两个交点分别为A(-1,0)、B(3,0), 与x轴的两个交点分别为A(-1,0)、B(3,0),
∴ 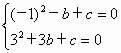 ,解之得 ,解之得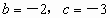 . .
∴所求抛物线的解析式为 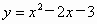 . .
(2) 设点P的坐标为(x,y),由题意,得
∴ |y|=4,∴y=±4.当 y=4时,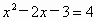
∴ 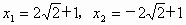 . .
当 y=-4时,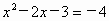 , ,
∴ x=1.∴满足条件的点 P有3个,即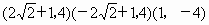 . .
(3) 在抛物线对称轴上存在点Q,使得△QAC的周长最小.∵ AC长为定值.∴要使△ QAC的周长最小,只需QA+DC最小,∵点 A关于对称轴x=1的对称点是B(3,0),∴由几何知识可知, Q是直线BC与对称轴x=1的交点.C点坐标是(0,-3)故设过点 B、C的直线的解析式为y=kx-3,∵直线过点 B(3,0),∴ 3k-3=0. ∴k=1,∴直线 BC的解析式为y=x-3.把 x=1代入上式,得y=-2,∴点Q坐标为(1,-2). |


科目:初中数学 来源: 题型:022
(2005 海南)如图所示,在△ABC中,∠C=90°,AC=3,D为BC
上一点,过点D作DE⊥BC交AB于E,若ED=1,BD=2,则DC的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:044
(2005·海南)如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于H.
(1)求证:①△BCG≌△DCE,②BH⊥DE.
(2)当点G运动到什么位置时,BH垂直平分DE?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com