试题分析:(1)由BE=AB-AE=12-2EF=12-2(CE-CF)=12-2(6-CF)=2CF即可求得结果;
(2)由BE=AB-AE=12-2EF=12-2(CE-CF)=12-2(6-CF)=2CF即可做出判断;
(3)设DE=x,则DF=3x,EF=2x,CF=6-x,BE=x+7,由(2)知:BE=2CF,即可列方程求得x的值,从而得到结果.
(1)∵F为AE的中点
∴AE=2EF
∴BE=AB-AE=12-2EF=12-2(CE-CF)=12-2(6-CF)=2CF
∴若CF=2,则BE=2,若CF=m,BE与CF的数量关系是BE=2CF;
(2)(1)中BE=2CF仍然成立.理由如下:
∵F为AE的中点
∴AE=2EF
∴BE=AB-AE=12-2EF=12-2(CE-CF)=12-2(6-CF)=2CF;
(3)存在,DF=3.理由如下:
设DE=x,则DF=3x
∴EF=2x,CF=6-x,BE=x+7
由(2)知:BE=2CF
∴x+7=2(6-x)
解得x="1"
∴DF=3,CF=5
∴
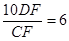
.
点评:解题的关键是熟练掌握线段的中点把线段分成相等的两条小线段,且都等于原线段的一半.

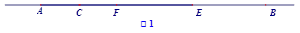
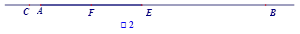
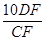 值;若不存在,请说明理由.
值;若不存在,请说明理由.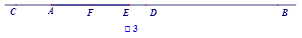
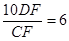
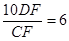 .
.

 名校课堂系列答案
名校课堂系列答案
