
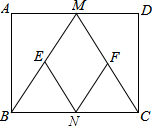
 如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD=1:2时,四边形MENF是正方形.
如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD=1:2时,四边形MENF是正方形. 分析 首先得出四边形MENF是平行四边形,再求出∠BMC=90°和ME=MF,根据正方形的判定推出即可.
解答 解:当AB:AD=1:2时,四边形MENF是正方形,
理由是:∵AB:AD=1:2,AM=DM,AB=CD,
∴AB=AM=DM=DC,
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,
∴∠BMC=90°,
∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°,
∴BM=CM,
∵N、E、F分别是BC、BM、CM的中点,
∴BE=CF,ME=MF,NF∥BM,NE∥CM,
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形,
即当AB:AD=1:2时,四边形MENF是正方形,
故答案为:1:2.
点评 本题考查了矩形的性质、正方形的判定、三角形的中位线的应用等知识,熟练应用正方形的判定方法是解题关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
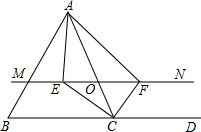 如图所示,△ABC中,点D在BC的延长线上,点O是AC边上的一个动点(不与A,C重合),过点O的直线MN∥BC,CE平分∠ACB交MN于点E,CF平分∠ACD交MN于点F.
如图所示,△ABC中,点D在BC的延长线上,点O是AC边上的一个动点(不与A,C重合),过点O的直线MN∥BC,CE平分∠ACB交MN于点E,CF平分∠ACD交MN于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
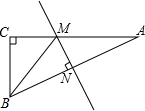 如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )| A. | 18 | B. | 16 | C. | 17 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
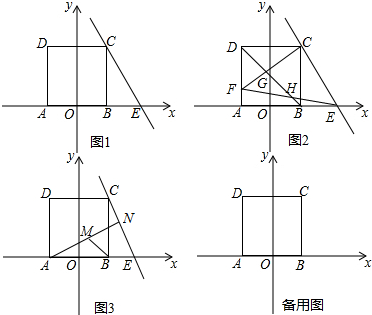
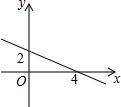 一次函数y=kx+b的图象,如图所示.
一次函数y=kx+b的图象,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com