
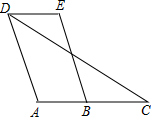
 已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.
已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.分析 根据平行线的判定得出AB∥DE,根据平行线的性质得出∠E=∠EBC,∠A=∠EBC,即可得出答案.
解答 证明:∵∠EDC=∠C,
∴AB∥DE(内错角相等,两直线平行),
∴∠E=∠EBC(两直线平行,内错角相等),
∵AD∥BE,
∴∠A=∠EBC(两直线平行,同位角相等),
∴∠A=∠E.(等量代换),
故答案为:DE,内错角相等,两直线平行,∠E,∠EBC,两直线平行,内错角相等,∠EBC,两直线平行,同位角相等.
点评 本题考查了平行线的性质和判定,能熟练地运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
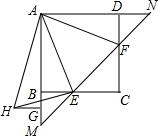 如图,在矩形ABCD中,点E、F分别在边BC、CD上,且EF分别与AB、AD的延长线交于点M、N,∠EAF=∠CEF=45°.点G在边AB的延长线上,将△ADF绕着点A按顺时针方向旋转90°后能与△AGH重合,连接EH.
如图,在矩形ABCD中,点E、F分别在边BC、CD上,且EF分别与AB、AD的延长线交于点M、N,∠EAF=∠CEF=45°.点G在边AB的延长线上,将△ADF绕着点A按顺时针方向旋转90°后能与△AGH重合,连接EH.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
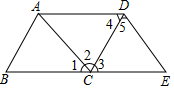 如图,点E在BC的延长线上,下列条件中,
如图,点E在BC的延长线上,下列条件中,| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com