
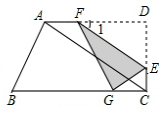
 ��ͼ�����ı���ABCD�У���D=��BCD=90�㣬��B=60�㣬AB=6��AD=9����E��CD�ϵ�һ�����㣨E����D�غϣ�������E��EF��AC����AD�ڵ�F����E�˶���Cʱ��EF��AC�غϣ����ѡ�DEF����EF���ۣ���D�Ķ�Ӧ���ǵ�G����DE=x����GEF���ı���ABCD�ص����ֵ����Ϊy��
��ͼ�����ı���ABCD�У���D=��BCD=90�㣬��B=60�㣬AB=6��AD=9����E��CD�ϵ�һ�����㣨E����D�غϣ�������E��EF��AC����AD�ڵ�F����E�˶���Cʱ��EF��AC�غϣ����ѡ�DEF����EF���ۣ���D�Ķ�Ӧ���ǵ�G����DE=x����GEF���ı���ABCD�ص����ֵ����Ϊy������ ��1����ͼ1����������AH��BC��AH�ij�����CD�ij�������ֱ���������е��������Ǻ���ֵ������AH�ij�����CD=AH=3$\sqrt{3}$����ֱ�ǡ�ACD�У����CAD=30�㣬��ƽ���ߵ�ͬλ����ȿ��Եá�1=��CAD=30�㣻
��2����ͼ2���ɶ��۵ã�Rt��FGE��Rt��FDE����GE=DE=x����FEG=��FED=60�㣬�Ӷ����ֱ�ǡ�GEC�У�EC=$\frac{1}{2}$x������DE+EC=CD ��ʽ�����x��ֵ��
��3������������
��һ�����Σ���$0��x��2\sqrt{3}$ʱ����ͼ3����GEF��ȫ���ı����ڲ��֣��ص�����������ǡ�GEF�������
�ڶ������Σ���$2\sqrt{3}$��x��$3\sqrt{3}$ʱ����ͼ4���ص������ǡ�GEF�����-��MNG�����������Ҫ������������Ǻ���ֵ��MG��NG�ij������������ʽ���ɣ�
�ٸ����������ε����ֵ���Աȵó������
��� 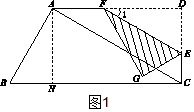 �⣺��1����ͼ1������A��AH��BC�ڵ�H��
�⣺��1����ͼ1������A��AH��BC�ڵ�H��
����Rt��AHB�У�AB=6����B=60�㣬
��AH=AB•sinB=6��$\frac{\sqrt{3}}{2}$=$3\sqrt{3}$��
�ߡ�D=��BCD=90�㣬
���ı���AHCDΪ���Σ�
��CD=AH=$3\sqrt{3}$��
��$tan��CAD=\frac{CD}{AD}=\frac{{3\sqrt{3}}}{9}=\frac{{\sqrt{3}}}{3}$��
���CAD=30�㣬
��EF��AC��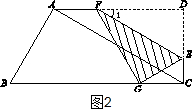
���1=��CAD=30�㣻
��2������Gǡ����BC�ϣ���ͼ2��
�ɶ��۵ĶԳ��Կ�֪Rt��FGE��Rt��FDE��
��GE=DE=x����FEG=��FED=60�㣬
���GEC=60�㣬
�ߡ�CEG��ֱ�������Σ�
���EGC=30�㣬
����Rt��CEG��EC=$\frac{1}{2}$EG=$\frac{1}{2}$x��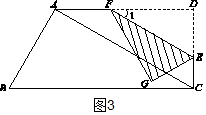
��DE+EC=CD ��$x+\frac{1}{2}x=3\sqrt{3}$��
��x=$2\sqrt{3}$��
��3������������
��һ�����Σ���$0��x��2\sqrt{3}$ʱ����ͼ3��
��Rt��DEF��tan��1=tan30��=$\frac{DE}{DF}$��
��DF=x��$\frac{\sqrt{3}}{3}$=$\sqrt{3}$x��
��y=S��EGF=S��EDF=$\frac{1}{2}•DE•DF$=$\frac{1}{2}•x•\sqrt{3}x$=$\frac{\sqrt{3}}{2}{x}^{2}$��
��$\frac{{\sqrt{3}}}{2}$��0���Գ���Ϊy�ᣬ
�൱$0��x��2\sqrt{3}$��y��x�����������
�൱x=$2\sqrt{3}$ʱ��y���ֵ=$\frac{\sqrt{3}}{2}$��$��2\sqrt{3}��^{2}$=$6\sqrt{3}$��
�ڶ������Σ���$2\sqrt{3}$��x��$3\sqrt{3}$ʱ����ͼ4��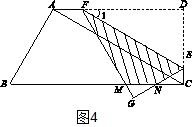
��FG��EG�ֱ�BC�ڵ�M��N��
����һ����DE=x��
��EC=$3\sqrt{3}-x$��NE=2$��{3\sqrt{3}-x}��$��
��NG=GE-NE=$x-2��{3\sqrt{3}-x}��$=$3x-6\sqrt{3}$��
�֡ߡ�MNG=��ENC=30�㣬��G=90�㣬
��MG=NG•tan30��=$\frac{{\sqrt{3}}}{3}��{3x-6\sqrt{3}}��$��
��${S_{��MNG}}=\frac{1}{2}•NG•MG=\frac{1}{2}��{3x-6\sqrt{3}}����\frac{{\sqrt{3}}}{3}��{3x-6\sqrt{3}}��$=$\frac{{\sqrt{3}}}{6}{��{3x-6\sqrt{3}}��^2}$
��y=S��EGF-S��MNG=$\frac{{\sqrt{3}}}{2}{x^2}-\frac{{\sqrt{3}}}{6}{��{3x-6\sqrt{3}}��^2}$=$-\sqrt{3}{x^2}+18x-18\sqrt{3}$
��$-\sqrt{3}��0$���Գ���Ϊֱ��$x=-\frac{18}{{2����{-\sqrt{3}}��}}=3\sqrt{3}$��
�൱$2\sqrt{3}$��x��$3\sqrt{3}$ʱ��y�����ֵ����y��x�����������
�൱$x=3\sqrt{3}$ʱ��${y_{���ֵ}}=\frac{{4��\sqrt{3}��18\sqrt{3}-{{18}^2}}}{{-4\sqrt{3}}}$=$9\sqrt{3}$��
�ۺ��������Σ�����$6\sqrt{3}$��$9\sqrt{3}$��
�൱$x=3\sqrt{3}$ʱ��y��ֵ���y�����ֵΪ$9\sqrt{3}$��
���� �������ı��ε��ۺ��⣬�������۵������ʡ����κ�������ֵ����������Ǻ���ֵ��ֱ����������30��ǵ����ʣ��������ص����ֵ������Ҫ�Ȱ�����λ�ö�Ӧ��x��ֵ��������ٷ�����������ۣ������Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 32��-23 | B�� | -23�� ��-2��3 | C�� | -32�루-3��2 | D�� | -3��2��32 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| -5 | A | B | C | D | E | F | x | G | H | P | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
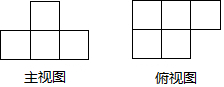
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
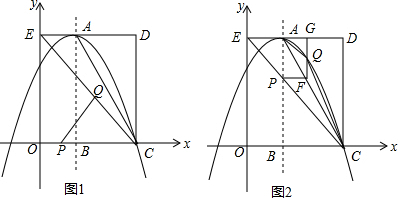
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com