
【题目】如图,△ABC在直角坐标系中
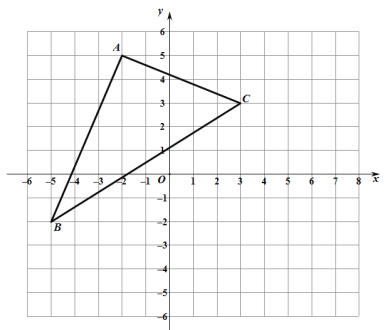
(1)请写出△ABC各点的坐标;
(2)求出△ABC的面积;
(3)如图,将三角形ABC向右平移3个单位长度,再向下平移2个单位长度,得到对应的三角形A1B1C1,并写出点A1、B1、C1的坐标
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
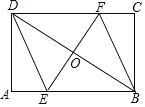
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
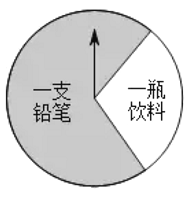
【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物![]() 元以上可以获得一次转动转 盘的机会,当转盘停止时指针落在哪一个区域就获得相应的奖品 (指针指向两个扇形的交线时,当作指向右边的扇形),下表是活动进行中的一组统计数据:
元以上可以获得一次转动转 盘的机会,当转盘停止时指针落在哪一个区域就获得相应的奖品 (指针指向两个扇形的交线时,当作指向右边的扇形),下表是活动进行中的一组统计数据:
转动转盘的次数 |
|
|
|
|
|
|
落在“铅笔"的次数 |
|
|
|
|
|
|
落在“铅笔"的频率 |
|
|
|
|
|
|
(1)转动该转盘一次,获得铅笔的概率约为____ ;( 结果保留小数点后一位数字);
(2)铅笔每只![]() 元,饮料每瓶
元,饮料每瓶![]() 元,经统计该商场每天约有
元,经统计该商场每天约有![]() 名顾各参加抽奖活动,请计算该商场每天需要支出的奖品费用;
名顾各参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在![]() 元左右,则转盘上“一瓶饮料”区域的圆心角应调整为 度.
元左右,则转盘上“一瓶饮料”区域的圆心角应调整为 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
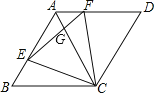
【题目】如图,菱形ABCD的边长为4,E,F分别是AB,AD边上的动点,BE=AF,∠BAD=120°,则下列结论:①△BEC≌△AFC;②△ECF为等边三角形;③∠AGE=∠AFC;④若AF=1,则![]() . 其中正确结论的序号有________.
. 其中正确结论的序号有________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
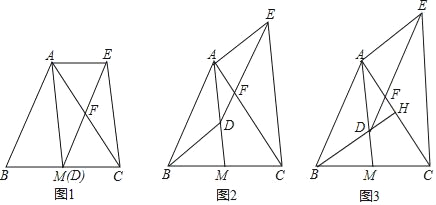
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM.
①求∠CAM的度数;
②当FH=![]() ,DM=4时,求DH的长.
,DM=4时,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
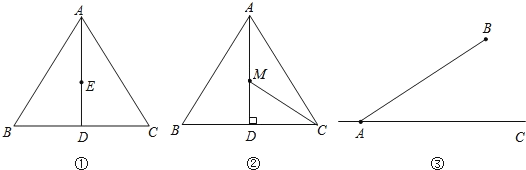
【题目】(问题探究)
(1)如图①,点E是正△ABC高AD上的一定点,请在AB上找一点F,使EF=![]() AE,并说明理由;
AE,并说明理由;
(2)如图②,点M是边长为2的正△ABC高AD上的一动点,求![]() AM+MC的最小值;
AM+MC的最小值;
(问题解决)
(3)如图③,A、B两地相距600km,AC是笔直地沿东西方向向两边延伸的一条铁路,点B到AC的最短距离为360km.今计划在铁路线AC上修一个中转站M,再在BM间修一条笔直的公路。如果同样的物资在每千米公路上的运费是铁路上的两倍。那么,为使通过铁路由A到M再通过公路由M到B的总运费达到最小值,请确定中转站M的位置,并求出AM的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“创科集团”会议室内的一个长为6米、宽为4米的矩形ABCD墙面需要进行装饰,设计图案如图所示,将矩形ABCD墙面分割成3个区域,中间“十”字形区域甲的宽度均为1米,四个角为四个全等的直角三角形,△AEF,△BGH,△CMN,△DPQ为区域乙,剩下部分为区域丙,其中AE=BG=CN=DP,设EG=HM=NP=FQ=x(米)(1≤x≤3)
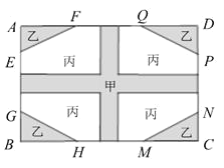
(1)当x=2时,求区域乙的面积;
(2)求区域丙的面积的最大值;
(3)为了图案富有美感,设置区域乙与区域丙的面积之比为1:4,在区域甲、区域乙、区域丙分别嵌贴甲、乙、丙三种不同的装饰板,这三种装饰板每平方米的单价分别为a(百元),b(百元),c(百元)(a,b,c均为整数,且6<a<10),若a+b+c=20,整个墙面嵌贴共花费了150(百元),求三种装饰板每平方米的单价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com