Question

10．如图，二次函数y=ax²+bx+c的图象与x轴交于点A（-2，0）和点B（4，0），与y轴交于点C（0，-4）．
（1）求二次函数的解析式，并写出抛物线的对称轴，顶点坐标；
（2）设E时抛物线对称轴上一点，当∠BEC=90°时，求点E的坐标；
（3）若P（m，n）是抛物线上一个动点（其中m＞0，n＜0），是否存在这样的点P，使得△PBC的面积最大？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

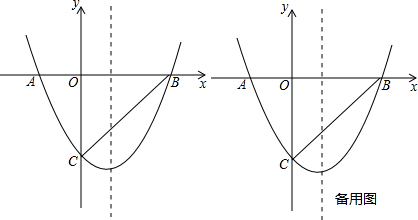
分析 （1）由点A、B、C三点的坐标利用待定系数法即可求出二次函数的解析式，再利用配方法将其化成顶点式即可找出该抛物线的对称轴及顶点坐标；
（2）设点E的坐标为（1，t），由两点间的距离公式可求出BE、CE、BC的长，根据勾股定理即可得出关于t的一元二次方程，解方程即可得出点E的坐标；
（3）由点P在抛物线上，可用m表示出n，由点B、C的坐标利用待定系数法即可求出直线BC的解析式，再由点到直线的距离求出点P到直线BC的距离，根据三角形的面积公式即可得出S_△PBC关于m的关系式，利用二次函数的性质即可解决最值问题．

解答 解：（1）将点A（-2，0）、B（4，0）、C（0，-4）代入y=ax²+bx+c中，
得$\left\{\begin{array}{l}{0=4a-2b+c}\\{0=16a+4b+c}\\{-4=c}\end{array}\right.$，解得：$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-1}\\{c=-4}\end{array}\right.$，
∴二次函数的解析式为y=$\frac{1}{2}$x²-x-4．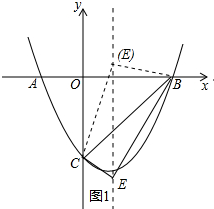
∵y=$\frac{1}{2}$x²-x-4=$\frac{1}{2}$（x-1）²-$\frac{9}{2}$，
∴该抛物线的对称轴为x=1，顶点坐标为（1，-$\frac{9}{2}$）．
（2）依照题意，画出图形，如图1所示．
设点E的坐标为（1，t），
∵B（4，0）、C（0，-4），
∴BE=$\sqrt{9+{t}^{2}}$，CE=$\sqrt{{t}^{2}+8t+17}$，BC=4$\sqrt{2}$，
∵∠BEC=90°，
∴BE²+CE²=BC²，即9+t²+t²+8t+17=32，
解得：t₁=-2+$\sqrt{7}$，t₂=-2-$\sqrt{7}$，
即点E的坐标为（1，-2-$\sqrt{7}$）或（1，-2+$\sqrt{7}$）．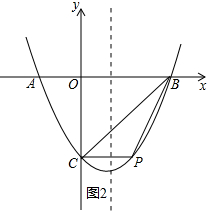
（3）假设存在，如图2所示．
∵P（m，n）是抛物线上一个动点（其中m＞0，n＜0），
∴n=$\frac{1}{2}$m²-m-4，0＜m＜4．
设直线BC的解析式为y=kx-4，
∵点B（4，0）为直线BC上的点，
∴0=4k-4，解得：k=1，
∴直线BC的解析式为y=x-4，即x-y-4=0．
点P到直线BC的距离d=$\frac{|m-\frac{1}{2}{m}^{2}+m+4-4|}{\sqrt{{1}^{2}+（-1）^{2}}}$=|-$\frac{\sqrt{2}}{4}$m²+$\sqrt{2}$m|，
∵0＜m＜4，
∴d=-$\frac{\sqrt{2}}{4}$m²+$\sqrt{2}$m．
S_△PBC=$\frac{1}{2}$BC•d=$\frac{1}{2}$×4$\sqrt{2}$×（-$\frac{\sqrt{2}}{4}$m²+$\sqrt{2}$m）=-m²+4m=-（m-2）²+4，
∴当m=2，即点P的坐标为（2，-4）时，S_△PBC取最大值4．
故存在这样的点P，使得△PBC的面积最大，点P的坐标为（2，-4）．

点评 本题考查了待定系数法求函数解析式、两点间的距离公式、三角形的面积公式以及二次函数的性质，解题的关键是：（1）利用待定系数法求出二次函数解析式；（2）根据勾股定理找出关于t的一元二次方程；（3）利用三角形的面积公式找出S_△PBC关于m的函数关系式．本题属于中档题，难度不大，解决该题型题目时，根据点的坐标，利用待定系数法求出函数解析式是关键．